Note: In honor of Tau Day, I'm re-posting and updating my original 2011 Tau Day post. Enjoy!

Happy Tau Day! Tau Day is today, but what exactly is it?

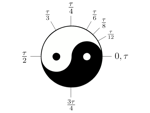
If you've been to this site before, you should be well acquainted with Pi. Like Pi (π), Tau (τ) is a a mathematical constant. The value is simple enough, in that it's 2π (2 × Pi).

Since Pi Day is 3/14, that makes Tau Day 6/28. So, why should we make such a big deal over Tau? That's the topic of today's Tau Day post!

Bob Palais started the ball rolling in 2001, with his editorial Pi Is Wrong! He wasn't talking about the actual number being a wrong quantity. When you divide a circle's circumference by it's diameter, you do get 3.1415... and so on. Palais' point was that it's the relationship to the diameter that's the basic problem.

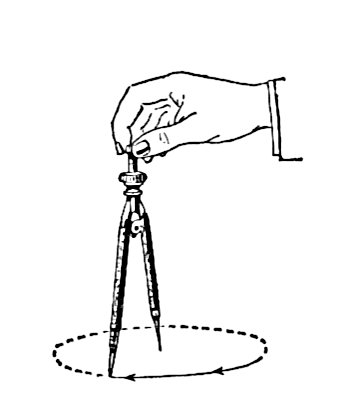Think about how you draw a circle with a compass. You place the spike at the center of your circle, and rotate the drawing implement around that point. You're taking advantage of the fact that every point on the circle is the same distance from the center of the circle.

In other words, you're taking advantage of the circle's radius, not it's diameter. Of course, if want the formula for a circle's circumference in relation to a radius (r), then you have 2πr. When you start working with the unit circle and radians (distance of the radius around the circumference), you run into 2π again, as the number of radians around a circle.

In formula after formula, 2π pops up again and again. To use Dr. C. Douglas Haessig's analogy, if Pi is a Hollywood star, then 2 is a constant groupie. Since Tau is 2 × Pi, Tau is basically the idea that these two have been dating for long enough, and it's time for them to get married.

What happens when we replace 2π with τ? I'll let Vihart, whose videos I recommended in an earlier post, explain further:



I tried to make radian conversion easy with a mnemonic (indeed, using this same video), but in the long run, you can see that Tau is a better way to go. Here are some handy links for further exploring the concepts in the above video:

• Intuitive Understanding of Sine Waves
• Intuitive Understanding Of Euler’s Formula
• The Tau Manifesto

Robert Dixon voices his support here, and even suggests replacing Pi with τ/2:



For a better understanding of how the area is being used here, check out The Story of Pi video, and A Gentle Introduction To Learning Calculus.

Back in November 2012, Numberphile discussed the advantages of this new approach in its Tau Replaces Pi video:



Numberphile fans being passionate in the way they think about numbers, this naturally led to an intense debate just over a month later:



Ultimately, Tau may offer a better future by offering a better understanding of mathematics, and that's definitely something worthy of celebration, and thus worthy of its own day.

This only leaves one problem. Tau is twice as much as Pi, but Tau's Greek letter has only half as many legs. Just for visual consistency, shouldn't π be 2τ, and τ be .5π? Just kidding, Tau Day fans.