Since we're about to switch over to a new calendar, how about some new calendar fun to go with it?

As many of you know, you can learn to give the day of the week for any date, and even practice the feat, right here on Grey Matters. If you want to make the work easier, there's my specially-prepared Day For Any Date Routine 2008 calendar, too.

The fact that calendars always have numbers in order and increase by 7 from week to week makes makes many mathematical tricks possible. A simple example would be having someone circle any 3 days in a row. Once they've done that, tell them to add up the 3 numbers they circled, and to give you the total. When you get the total, simply divide it by 3, and that will tell you the middle date. The other two dates, of course, are the ones immediately before and after it. If they gave you a total of 48, you divide it by 3 to get 16. This tells you that they chose the dates 15, 16 and 17. This will also work with columns, too, but you'll have to add an subtract 7 for the remaining two days. If they give you 57, you divide it by 3 and get 19, which tells you that they chose 12, 19 and 26!

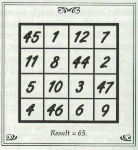
What about other arrangements of numbers? Here's an article that starts by teaching you a simple calendar feat with a square group of numbers, and proceeds to show you how to design your own custom calendar tricks using the same approach! If you understand the algebra well enough, you might be able to work out this trick before clicking on its secret.

Instead of trying to find out chosen dates from a total, you can go the opposite direction, too. Here are two impressive routines, in which you apparently add up a group of numbers from the calendar faster than your audience member can with a calculator.

What if you want to make a calendar routine seem more magical than mathematical? If you have Java installed in your browser, try out this bit of Calendar Magic from Cut-The-Knot.

Martin Gardner's Mathematics, Magic and Mystery has a great section on Calendar Magic. If you click on that last link and scroll down, you'll see one of the most magical calendar routines by Walter Gibson (creator of The Shadow!), called Gibson's Circled Dates. This routine involves circling dates that are unknown to you, yet you're still able to give their total. Milbourne Christopher wrote up a great stage presentation for this feat called Super Date Sense.

Back in the May 1999 issue of MAGIC Magazine, Bob Farmer published his version of a calendar idea originally developed by Robin Dawes. Instead of a lightning calculation or a magic trick, this takes the form of a game. A marker is placed on January 1st of any calendar, and two players take turns alternating moves. There are only two legal moves. A player can either move the marker to any later date in the same month, or the same date in a later month. The person who moves the marker onto December 31st is the winner.

Try playing this game against the computer. After a few games, you'll realize that the computer is winning every time. If you study the moves made by the computer closely enough, you'll be able to work out why those moves are chosen, and why they win the game every time. You can even play the game backwards, and only a minor alteration in the math is required to win every time. Here's one hint: The math required to win every time at this calendar game is so simple that, once you've mastered it, you can play the game with no calendar at all, and just call out the dates verbally!

Now you know myriad ways to amuse, amaze and even cheat with a calendar. Go out, have some fun with these, and have a happy new year!

Richard Wiseman has just released a new book called Quirkology.

Grey Matter readers will remember him from his magic square performance video. Many others will remember him from his amazing color changing card trick video:

This video, as it happens, is an excellent example of what the book, and the Quirkology site, is all about. From the site:

'Quirkology' is a term coined by Prof Wiseman to refer to psychological research that is quirky. Much of this work uses mainstream methods to investigate unusual topics, or unusual methods to investigate mainstream topics.

The best way to get an idea of exactly what this means is to participate in some of the live experiments yourself (UK link), or even some of the past experiments (UK link)!

Any who knows me will tell you I am a big fan of all things quirky and whimsical. Beyond just being quirky for quirkiness' sake, however, Quirkology looks into these ideas analytically. The scientific search for the world's funniest joke is about much more than just which joke is truly the funniest one, but about what can be learned in the search. Check out the introduction (UK link) for a better idea of the book.

If you relate quirky ideas to magic tricks (as happens in the book), then I'd describe this not as learning how a magic trick works, but rather why the magic tricks work, and how they are perceived. For a student of human nature and ideas, Quirkology ranks right up there with Made To Stick.

I didn't want to get into any heavy memory or math techniques or applications for a holiday entry. Instead, I'm going to blatantly steal an idea from the Christmas 2006 episode of Mythbusters, and simply demonstrate a few mind-boggling Rube Goldberg mahcines for you.

A Rube Goldberg machine, for those of you unfamiliar with the term, is a machine that performs a simple task in a needlessly complex and convoluted manner. They're name for Rube Goldberg, a cartoonist who was famous for drawing such machines. It's somewhat appropriate we're doing this in December, as he passed away in December of 1970.

Since I'm blatantly stealing the idea from Mythbusters, I should at least demonstrate the idea by giving their contraption center stage:

Among the most creative Rube Goldberg machines I've found on the web are:
* 3-D animated tribute to Rube Goldberg and Nintendo
* Incredible intros for a Japanese TV show called That's the Way Things Go
* A German beer commercial that features an unusual trap
* Guiness' $20 million Tipping Point Ad

Probably the most incredible Rube Goldberg machine to date, would have to be the one from Honda's now-famous ad, The Cog, which used two complete Honda Accords, and took 606 takes to get right!



Happy Holidays!

As the year draws to a close, plenty of Grey Matters favorites seem to be putting in one last 2007 appearance. For example, I've recently found a new online video featuring Arthur Benjamin.

Over at Online Visions, Werner Miller is back with a mathematical twist on an old idea, which he called A Holey Number. Werner Miller seems to have a particular fondness for creative approaches to magic squares, as his Square Bet and Age Cube demonstrate.

The first simple challenge of A Holey Number is to put four puzzle pieces together to make a magic square. This is easily done, and results in a magic square whose rows, columns and diagonals add up to 30. The four pieces are then picked up, mixed, and turned over. The same challenge is given. This time, there's a big surprise. The magic square still totals 30, but when the puzzle is assembled, the 0 is replaced by an empty space!

As mentioned in the first paragraph of the article, this is presented as a puzzle or paradox. If you want to, as Werner Miller puts it, “have a strange piece of story-telling magic”, then you can alter the presentation. For a puzzle-based routine like this, a great place to start would be the works of Robert Neale (especially The Magic Mirror) or Stewart James. My Memorable Magic series of posts could also be helpful here.

As it happens, the pattern used in A Holey Number can be arranged on a standard 15 puzzle. Due to this, you might consider mixing A Holey Number with my 40 30s 4 15 routine (video clip).

One way to present this would be as a farcical race, to see who could be the first to see who can make a magic square with 15 numbers. Since you as the performer has to work with 15 sliding tiles (and get them into the 11, empty space, 7, 12 pattern), and the spectator has to work with only the four pieces of the red side. After they've obviously already finished, you finish arranging the 15 puzzle and facetiously declare victory. When it's pointed out that the spectator finished first, you hesitate, while trying to think of a way out of this. Then, you remember that you specified that the magic square should be made with 15 numbers, showing that you really did use only 15, and their four-piece puzzle involved 16 numbers (uh, yeah, that's it! That's the ticket!). Give them a second chance to beat you, pick up the four pieces, turn them over to the blue side, and have them arrange those pieces. Since they have shown how quickly they can do it, and it was still faster than your 15 puzzle time, you finally admit they're the winner, leaving them puzzled as to why the 0 is an empty space now.

If you have any other presentation ideas for A Holey Number, I'd love to hear about them in the comments!

Since the focus of this blog is largely math and memory feats, it probably won't be a surprise to learn that my favorite Christmas carol is The 12 Days of Christmas. After all, it's got a long list and it's full of numbers!

On the extremely unlikely chance you haven't heard this song too many times already this holiday season, here's John Denver and the Muppets singing The 12 Days of Christmas:

The memory part is usually what creates the most trouble. In the above video, Fozzie has trouble remembering what is given on the 7th day. Even a singing group as mathematically precise as the Klein Four Group has trouble remembering what goes where in their version of The 12 Days of Christmas:



Just to make sure that you've got them down, I'll give you 5 minutes to correctly name all of the 12 Days of Christmas gifts. Those of you who have been practicing this quiz since I first mentioned it in last Sunday's post will have an advantage.

Now that we've got the memory part down, I'll turn to the math. What is the total number of gifts are being given in the song? 1+2+3 and so on up to 12 doesn't seem easy to do mentally, but it is if you see the pattern. Note that 1+12=13. So what? So does 2+11, 3+10 and all the numbers up to 6+7. In other words, we have 6 pairs of 13, and 6 times 13 is easy. That gives us 78 gifts total.

As noted in Peter Chou's Twelve Days Christmas Tree page (whose icon is at the top left of this post), the gifts can be arranged in a triangular fashion, since each day includes one more gift than the previous day. Besides being aesthetically pleasing, it turns out that a particular type of triangle, Pascal's Triangle, is a great way to study mathematical questions about the 12 days of Christmas.

First, let's get a Pascal's Triangle with 14 rows (opens in new window), so we can look at what it tells us. As we discuss these patterns, I'm going to refer to going down the right diagonal, but since the pattern is symmetrical, the left would work just as well.

Starting with the rightmost diagonal, we see it is all 1's. This represents each day's increase in the number of presents, since each day increases by 1. Moving to the second diagonal from the right, we see the simple sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12, which can naturally represent the number of gifts given on each day of Christmas.

The third diagonal from the right has the rather unusual sequence of 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91. This is a pattern of triangular numbers.

But what can triangular numbers tell us about the 12 days of Christmas? If you look at where the 3 in this diagonal, it's southwest (down and to the left) of the 2 in the second rightmost diagonal. If, on the 2nd day of Christmas, you gave 2 turtle doves and 1 partridge in a pear tree, you would indeed have given 3 gifts, but does the pattern hold? On the 3rd day, you would have given 3+2+1 (3 French hens, 2 turtle doves and a partridge in a pear tree) or 6 gifts total, and sure enough, 6 can be found southwest of the 3! For any of the 12 days, simply find that number, and look to the southwest of that number to see how many gifts you've given by that point! Remember when figured out that the numbers 1 through 12, when added, totaled 78? Look southwest of the 12, and you'll find that same 78!

Let's get really picky and technical about the 12 days of Christmas. It clearly states that on the first day, your true love gave you a partridge in a pear tree, and on the second day your true love gave you two turtle doves and a partridge in a pear tree. You would actually have 4 gifts (counting each partridge and its respective pear tree as one gift) by the second day, the first day's partridge, the second day's partridge and two turtle doves. By the third day, you would have 10 gifts, consisting of 3 partridges, 4 turtle doves and 3 French hens.

At this rate, how many gifts would you have at the end of the 12th day? Sure enough, the pattern of 1, 4, 10 and so on, known as tetrahedral numbers (Java required, opens in new window), can be found in our Pascal's Triangle as the 4th diagonal from the right.

If you look at the 2nd rightmost diagonal, you'll see the number 2, and you'll see the number 4 two steps southwest (two steps down and to the left) of it, which tells us you'll have 4 gifts on the second day. Using this same method, you can easily see that you'll have 10 gifts on the 3rd day, 20 gifts on the 4th day, and so on. If you really did get gifts from your true love in this picky and technical way, you would wind up with 364 gifts on the 12th day! In other words, you would get 1 gift for every day in the year, not including Christmas itself (also not including February 29th, if we're talking about leap years)!

If you're having any trouble visualizing any of this so far, Judy Brown's Twelve Days of Christmas and Pascal's Triangle page will be of great help.

One other interesting pattern I'd like to bring up is the one that happens if you darken only the odd-numbered cells in Pascal's Triangle. You get a fractal pattern known as the Sierpinski Sieve. No, this won't tell you too much about the 12 days of Christmas, except maybe the occurrences of the odd days, but it can make a beautiful and original Christmas ornament! If you have kids who ask about it, you can always give them the book The Number Devil, which describes both Pascal's Triangle and Sierpinski Sieve, among other mathematical concepts, in a very kid-friendly way.

There's another 12 Days of Christmas calculation that's far more traditional: How much would the 12 gifts actually cost if you bought them? According to the Motley Fool, the 12 gifts of Christmas would cost a total of US$78,100! If you wanted to cut your costs and buy just one of each, you would still have to shell out US$19,507!

Since my Christmas spending is done, I'm going to have to forgo the expensive version, in favor of Miss Cellania's internet-style version of The 12 Days of Christmas. Happy Holidays!

Since it's the holiday season, I've been turned my attention classics and toys. One of the classics that used to puzzle me in my youth was the classic game of Mastermind^TM.

This is the classic two-person game in which one person sets up a code consisting of four colored pegs, chosen from among 6 different colors. Since repeating colors in the code is allowed, this means that the code could be any one of 1,296 (6 * 6 * 6 * 6) possibilities. The other player has 10 guesses to figure out the code. The only clues this player gets from the person who set up the code is in the form of black and white "clue pegs". For every correct color the guesser has in the correct spot, they are given 1 black clue peg. For every correct color the guesser has in the wrong spot, they are given 1 white clue peg.

Interpreting the clues from your current guess, combined with the clues provided in earlier guesses, becomes an exercise in logic. What colors are always in my correct guesses, and which colors aren't?

If you would like to put your mind up against this test, I've added it to the site! In the Mental Gym, you can now find a Java version of Mastermind^TM (In this version, you only have 8 guesses). If you would prefer to play it on your iPhone or iPod Touch, I've added a link to the game SuperBrain (opens in new window) to the iPhone Mental Gym.

If you prefer the real board game, perhaps as a gift, I've also added the Mastermind^TM Travel Attache set to the Recommended Products Store.

Once you've tried it out in one form or another, you're probably asking yourself, is it really possible to narrow the code down from 1,296 possibilities in only 10 guesses, even with the clues you get? Believe it or not, not only is it possible, but when played correctly, you will never need more than 5 guesses to break the code!

In the earlier Mastermind^TM Wikipedia entry, there is a brief discussion of the five guess algorithm. If you would like to learn more about it, Toby Nelson's Investigations into the Mastermind^TM Board Game is an excellent resource. It describes the mathematical basics of the game, and then goes into the hows and whys of the algorithm itself. Fortunately, this is all done in clear language, and is easy to follow. Once you understand the basic ideas, Mr. Nelson even provides a strategy table, showing how every code can be resolved in 5 moves or less.

My suggestion is not to peek at this approach, but try playing the game first. See if you can arrive at some of your own strategies before looking at the algorithms. Good luck and happy decoding!

Note: Many people have found this entry while searching for “Websites Like Sporcle”. If that's what you're searching for, then check out my How Many Xs Can You Name In Y Minutes? post. It lists thousands of quizzes on Sporcle and sites like Sporcle!

If you've enjoyed brain training, here are some new ways to challenge your brain!

I'll start with an update. Back in October, I mentioned Sporcle's free online games. At the time there was just the geography challenges, the US presidents, Shakespeare's plays, and the Super Bowl winners. Since that time, they've added many more challenges to their games section! Can you name all of the TOS Star Trek crew, the TNG Star Trek crew, NATO alphabet words, UK Prime Ministers, Las Vegas Strip casinos, Tom Hanks movies, or US state capitals? During the Christmas season, they also have a challenge where you must name all 12 gifts from the song The Twelve Days of Christmas in order from 1 to 12! This is trickier than it sounds, because they're usually sung in order from 12 to 1.

If you like Sporcle's geography challenges, but find them too easy, then you might want to try Traveler IQ. In this one, you have to click on various cities, landmarks and more, and you're awarded points both for how close your click was to the actual location, as well as how quickly you click. To pass each level, you must get a minimum number of points. As you progress, the game also keeps track of your Traveler IQ (100 is average), so you can see how well you're doing compared to others.

This next challenge is unlike almost any other one I've ever seen. It's called Sprout. All I can say is try it! To explain anything about it would be to rob you of the joy of discovery that is the hallmark of the game.

It's about time we had some math in here to challenge you brain, so here it is. The math challenge is Brain Tower, and it features an unusual interface. Instead of clicking on anything, you figure out the answer, and entering in the format http://alexbrie.net/braintower/problem_number/answer. The answer to the first question is 1, so you would type the new address in as http://alexbrie.net/braintower/1/1. The answer to the second question is 10 (no, I'm not really giving anything away here), so you would type http://alexbrie.net/braintower/2/10, and so on. The challenge is to work your way up through all 25 levels of the Brain Tower this way.

I'll finish with Gameloft's newest release, called Brain Challenge. If you've seen Brain Training on other platforms, and hoped for it on your iPod classic, iPod video and the 3rd generation iPod nano, you can now get Brain Challenge on iTunes for $4.99.

When you start, there are 5 brain challenges, and by playing and getting better at these, you can unlock 15 more challenges, as well as some creativity exercises. Here's a preview of the iPod version of Brain Challenge:

So far, my only criticism of Brain Challenge is that it starts right out with my pet peeve: claiming that we only use 10% of our brains. The debunking of this myth by Snopes and The Straight Dope haven't done much to curb its use. To be fair, this myth is used to introduce the scoring system. Instead of Brain Age, as in the game of the same name, Brain Challenge gives your overall score as a percentage of your brain power.

One thing I like about this game is that, even though it's being released for the iPod, Xbos, PC and Nintendo DS, Gameloft is paying particular attention to the interfaces of each device, and designing the games to the strengths of the respective interfaces.

Do you have any other brain-challenging games you would like to share? Let everyone know in the comments!

While memory feats can be amazing on their own, a reason for performing them can help make them far more interesting to your audiences. Here are a few plots I've come up with to use as starting points for memory feat presentations. I developed these on my own, and they're original as far as I know.

The first plot is a way to get two feats for the price of one. For this, you have to know how to do the Day of the Week For Any Date feat, and any 4 by 4 magic square routine in which the spectator starts by giving you 4 numbers to use in the square. You can find routines like this in Mathematical Wizardry, Mark Farrar's How To Create A Birthday Magic Square ebook, or Chuck Hickock's Diagonal Magic Square (now out of print).

You start by asking for someone's birthday, give the day of the week for it, and have the day of the week verified via a perpetual calendar. Mention that you're often asked how you figure the day of the week so quickly. Explaining that it's not so much a particular process, you explain that you simply see the numbers come together, much like in the movie A Beautiful Mind, or the TV show Numb3rs. You bring out a board marked with a 4 by 4 grid, and say that you're going to give them an idea of what happens when you think of the dates. You ask for a new birthday from someone, and fill those in as the 4 starting numbers in the grid. For example, if they say their birthday is October 12, 1974, you write the numbers 10 (October), 12, 19 (first 2 digits of the year) and 74 (last 2 digits of the year) in different boxes, according to the particular magic square method you're using. As you're writing the numbers, you figure out the day of the week for the date, and remember that for later.

Reminding them of how the numbers come together in your mind, you quickly fill out the rest of the squares. Once you're finished, you say, "...and this is how I know that this date falls on..." and give the correct day of the week (Saturday, in our October 12, 1974 example). Once the day is verified, you explain that part of the reason you knew this date was correct was that the numbers that flash in your head allow you to verify the answer from different perspectives. To explain, you show that all the seemingly-random numbers on the grid give the same total when added horizontally, vertically, diagonally and so on.

This plot is great for giving a Rain Man type of impression. For a larger audience, you could use a pre-made grid, such as Meir Yedid's Total Destiny. However, you can make it more theatrical with the use of a transparent dry-erase board, which will build the suspense as they see the numbers written backwards, and imposed on your face. There are some great discussions on the use of transparent dry-erase boards for routines like this in the Mentalist Sanctum and the members-only section of the Magic Cafe.

The second plot is simply the idea of a book puppet, which you claim is an almanac, an atlas or whatever type of book would have the information you've memorized. The book puppet effectively acts as the source for the answers you give in your memory feat. This is a small idea with many advantages. The book can be used for a metaphor restriction violation (see vol. 1 of Wonder Words), which is the technical term for attributing powers, actions or thoughts to something, the book puppet in this case, that obviously can't possess them. The effect of this is that the audience sees through this claim, and attributes the amazing recall of facts. Since this is done both subconciously and indirectly, it's much more effective and enjoyable than directly claiming an amazing memory. In the show Dr. Wilson's Memory Elixir, a drink with apparent memory-improving qualities is used in the same way.

Also, if you need to take the time to recall the information, you can have the book apparently whisper the answer to you. You can get a brief comedic moment by seeming to forget the information, and having the book remind you. Getting into a contest where you compete against the book to see who can answer more questions from the audience correctly could be very funny.

If any of you have any great plots for memory, math or other brain-related feats you would like to share, please include them in the comments!

It's holiday time once again! If you're looking for brain straining and entertaining gift ideas, you've come to the right place! Even better, many of the links I'll share with you will allow you to compare prices, so you can get the best deal on those gifts which strike your fancy.

I live in Las Vegas, so I'm going to start close to home. Back in the late '80s and early '90s, a team of students and faculty from MIT formed a blackjack team that used mathematics, memory training, and nerve to take Las Vegas' blackjack tables for millions! The History Channel produced a documentary about the MIT blackjack team titled Breaking Vegas. One of the original team members, Ben Mezrich, has even written a detailed account of his time with the team, calling his book Bringing Down The House. We've all fantasized about winning millions in Vegas, and these true accounts show just what it takes, as well as the rewards and consequences.

Among the biggest news in entertainment this season is the return of Futurama! Among its fans, Futurama is known for including numerous examples of mathematical humor, some of it very advanced! If you know (or are) a Futurama fan, you can get caught up with the series by picking up vols. 1, 2, 3 and 4 of the series.

Once they're caught up, check out the newly-released Futurama movie, Bender's Big Score! The 90-minute movie opens, not surprisingly, with humorous references to their being canceled. After a few jabs at FOX, naked spamming aliens take control of Bender and make him travel through time to steal histories greatest treasures! Don't believe me? Check out the trailer! Among the bonuses on the DVD are a math lecture from the FuturamaMath.com team, called Bite My Shiny Metal X, a complete episode of Everybody Loves Hypnotoad, A Terrifying Message from Al Gore, and much more!

Of course, I can't mention popular math-based shows without mentioning Numb3rs! Now in its 4th season, it's proved that math can be entertaining, interesting and useful. Seasons 1, 2 and 3 are now available on DVD. The Charlievision sequences that help explain the mathematical concepts have proved especially popular with fans and educators. For those who want to learn more about the math explored in the first 3 seasons, the book Numbers behind Numb3rs: Solving Crime with Mathematics provides more details about them.

It's one thing learning about somebody else's skills in math and/or memory. Maybe you're interested in improving your own skill in these areas as part of your New Year's resolutions. But how do you go about it?

There are many fun ways to improve your memory, but as starting points, I would highly recommend the Harry Lorayne classics, The Memory Book and Super Power Memory.

For practicing the memory techniques you learn, I'm going to shamelessly self-promote my own memory training CD-ROM, Train Your Brain and Entertain (TYBE), available for both Mac OS X (view Flash demo) and Windows (view Flash demo). If you would like to try before you buy, try out the free lite version. You can download TYBELite for Mac here, and you can download TYBELite for Windows here. If you decide you like the software, but you believe it is too late to get the CD-ROM in time, it's also available for purchase as a download!

How about math? Wouldn't it be great to get better and faster at math? For improving your speed math skills, I highly recommend Secrets of Mental Math, Math Magic, Speed Mathematics and the classic Trachtenberg Speed System of Basic Mathematics.

Speed math is one thing, but how do you make math in general interesting enough to inspire further exploration? As anyone who knows will tell you, the best answer are the books of Martin Gardner. A good place to start is with his book Mathematics, Magic and Mystery, which uses magic tricks to inspire interest in mathematical principles. Martin Gardner's collections of his Scientific American columns, such as Hexaflexagons and Other Mathematical Diversions, Second Scientific American Book of Mathematical Puzzles and Diversions, and The Unexpected Hanging and Other Mathematical Diversions, are great ways to dive into math.

Martin Gardner isn't the only author who can make math fun, though. If you have a daughter in middle school who is struggling with math, Danica McKellar (whom you may remember as Winnie Cooper on The Wonder Years) has written a book called Math Doesn't Suck: How to Survive Middle-School Math Without Losing Your Mind or Breaking a Nail. For the more advanced math student, Prisoner's Dilemma is a fascinating study of John von Neumann's development of game theory. I posted about the basics of the Prisoner's Dilemma back in May, but this book goes deeper into it, discussing the effect this dilemma had on everything from simple everyday human interactions all the way up to the atomic bomb and the cold war!

Reading isn't the only way to better yourself! If your loved one is into brain training, how about giving them a black and crimson Nintendo DS Lite that comes bundled with Brain Age²? They'll also be able to play the original Brain Age and Big Brain Academy on it, as well!

Let's not forget about gifts that keep on giving. You can keep your loved ones smart all year with subscriptions to magazines like GAMES, Scientific American Mind and Mental Floss (a personal favorite).

If you have a loved one who regularly read Grey Matters or similar sites, please take a look around the Grey Matters recommended products store, which allows you to compare prices on popular items, and the Grey Matters original products store, where you'll find unique gifts that aren't available anywhere else. Happy holidays!