This post and the next are about handy mnemonics for trigonometry. For both of them, I'm going to assume you're familiar with the unit circle and Pi.

We'll start off with Vi Hart's rant about Pi being wrong. This is a conviction shared by Michael Hartl and Bob Palais, among others:



If the part about Euler's identity confuses you, check out BetterExplained.com's Intuitive Understanding Of Euler’s Formula.

My own solution to this problem is to preserve Pi, and just switch to “diameterians”, a unit of measure equal to 2 radians. Even if we eventually do switch to Tau or diameterians, the switch isn't going to happen anytime soon. Until that time, we need a way to remember facts about the unit circle relating to the way they're taught now.

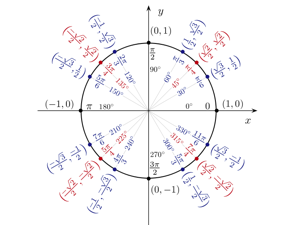
Without knowing it, Vi Hart has inspired an idea in me for a mnemonic to help convert from degrees to radians easily. The trick is to first think about a measure in “pies”, as if you were considering how much Pi is left, and then to think about the measure in Pi.

Let's start with a simple example, that of 180° (degrees). How many radians is that? Well, if you had an actual pie, and only 180° was left, you only have half of a pie. Put more formally, you have:



It may sound ridiculous, but I'm always going to be using the plural phrase, “in pies”, because it's going to help lock in the mnemonic. I'll explain that shortly, but first we need a starting point.

If you're given any multiple of 90°, it's pretty easy to picture these in pies, as it was how many of us were taught:



45° isn't much harder, especially considering that we've already dealt with half of them above. You just have to remember that 45° is 1/8 of a pie. Here are the rest:



The last set of multiples you usually need to know when dealing with the unit circle is 30°, or 1/12 of a circle. Without duplicating any of the above, here are the final fractions:



As you're about to see, if you can convert degrees into a fractions of pies, you're most of the way there.

When changing the word from “pies” to “pi”, we have to chop off half of the letters, don't we? Similarly, we halve to chop the fraction in half. This is the handy mnemonic I promised you earlier. To convert from “in pies” to “in pi” we have to chop off half the letters and half the value of the fraction.

How do we go about this? It's simple, just take the denominator (the bottom number of the fraction), and divide it by two. When dealing with 4ths, 8th or 12ths as above, this will always be possible. Let's try this with 90°:



See? It's easy! Now, in the unit circle, Pi is always put on the top of the fraction, so we should actually do it this way:



Trying this with a tricker number, such as 315°, once you get the fraction in pies, is just as easy:



In short, if you remember to convert from pies to pi by cutting the letters in half, you can remember to cut the number on the bottom of the fraction in half, as well. When dealing with the common amounts of 30°, 45°, 90° and their multiples, this works well.

What happens when you come up with a more unusual angle, such as 216°? Let's try it and find out:



We're still in pies, and we've run into a problem? If we divide by 2 to convert from pies to pi, we'll wind up with 3/2.5! It's one thing to reduce fractions, but that's going a little far.

In this case, we use the alternative approach of doubling the numerator (top number of the fraction). Continuing in this manner, we get:



To help remember which number you double and which number you divide by two, here's another mnemonic: You can make the Lower number Lesser, and the Higher number more Humongous. Alternatively, you could think of making the Lower number Lighter and the Higher number Heavier.

Practice this, and you'll soon have no problem converting degrees to radians in your head. Once you've got this down, you also shouldn't have any problem converting radians to degrees, as well.

Since, in this case, you're going from pi to pies thus doubling the number of letters, you'll be doubling the denominator, as well. Let's try to figure out Pi/12 radians in degrees:



That covers degree and radian conversion in your head. In Sunday's post, you'll learn how to calculate sine and cosine on your fingers! (No, I'm not kidding.)