 Note: This post first appeared on Grey Matters in 2007. Since then, I've made it a sort of annual tradition to post it every December, with the occasional update. Enjoy!
Note: This post first appeared on Grey Matters in 2007. Since then, I've made it a sort of annual tradition to post it every December, with the occasional update. Enjoy!
Since the focus of this blog is largely math and memory feats, it probably won't be a surprise to learn that my favorite Christmas carol is The 12 Days of Christmas. After all, it's got a long list and it's full of numbers!
On the extremely unlikely chance you haven't heard this song too many times already this holiday season, here's John Denver and the Muppets singing The 12 Days of Christmas:
The memory part is usually what creates the most trouble. In the above video, Fozzie has trouble remembering what is given on the 7th day. Even a singing group as mathematically precise as the Klein Four Group has trouble remembering what goes where in their version of The 12 Days of Christmas (Their cover of the Straight No Chaser version):
Just to make sure that you've got them down, I'll give you 5 minutes to correctly name all of the 12 Days of Christmas gifts. Those of you who have been practicing this quiz since I first mentioned it back in 2007 will have an advantage.
Now that we've got the memory part down, I'll turn to the math. What is the total number of gifts are being given in the song? 1+2+3 and so on up to 12 doesn't seem easy to do mentally, but it is if you see the pattern. Note that 1+12=13. So what? So does 2+11, 3+10 and all the numbers up to 6+7. In other words, we have 6 pairs of 13, and 6 times 13 is easy. That gives us 78 gifts total.
As noted in Peter Chou's Twelve Days Christmas Tree page, the gifts can be arranged in a triangular fashion, since each day includes one more gift than the previous day. Besides being aesthetically pleasing, it turns out that a particular type of triangle, Pascal's Triangle, is a great way to study mathematical questions about the 12 days of Christmas.
First, let's get a Pascal's Triangle with 14 rows (opens in new window), so we can look at what it tells us. As we discuss these patterns, I'm going to refer to going down the right diagonal, but since the pattern is symmetrical, the left would work just as well.
Starting with the rightmost diagonal, we see it is all 1's. This represents each day's increase in the number of presents, since each day increases by 1. Moving to the second diagonal from the right, we see the simple sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12, which can naturally represent the number of gifts given on each day of Christmas.
The third diagonal from the right has the rather unusual sequence of 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91. This is a pattern of triangular numbers.
But what can triangular numbers tell us about the 12 days of Christmas? If you look at where the 3 in this diagonal, it's southwest (down and to the left) of the 2 in the second rightmost diagonal. If, on the 2nd day of Christmas, you gave 2 turtle doves and 1 partridge in a pear tree, you would indeed have given 3 gifts, but does the pattern hold? On the 3rd day, you would have given 3+2+1 (3 French hens, 2 turtle doves and a partridge in a pear tree) or 6 gifts total, and sure enough, 6 can be found southwest of the 3! For any of the 12 days, simply find that number, and look to the southwest of that number to see how many gifts you've given by that point! Remember when figured out that the numbers 1 through 12, when added, totaled 78? Look southwest of the 12, and you'll find that same 78!
Let's get really picky and technical about the 12 days of Christmas. It clearly states that on the first day, your true love gave you a partridge in a pear tree, and on the second day your true love gave you two turtle doves and a partridge in a pear tree. You would actually have 4 gifts (counting each partridge and its respective pear tree as one gift) by the second day, the first day's partridge, the second day's partridge and two turtle doves. By the third day, you would have 10 gifts, consisting of 3 partridges, 4 turtle doves and 3 French hens.
At this rate, how many gifts would you have at the end of the 12th day? Sure enough, the pattern of 1, 4, 10 and so on, known as tetrahedral numbers, can be found in our Pascal's Triangle as the 4th diagonal from the right.
If you look at the 2nd rightmost diagonal, you'll see the number 2, and you'll see the number 4 two steps southwest (two steps down and to the left) of it, which tells us you'll have 4 gifts on the second day. Using this same method, you can easily see that you'll have 10 gifts on the 3rd day, 20 gifts on the 4th day, and so on. If you really did get gifts from your true love in this picky and technical way, you would wind up with 364 gifts on the 12th day! In other words, you would get 1 gift for every day in the year, not including Christmas itself (also not including February 29th, if we're talking about leap years)! Below is the mathematical equivalent of this calculation:
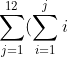=364)
If you're having any trouble visualizing any of this so far, Judy Brown's Twelve Days of Christmas and Pascal's Triangle page will be of great help.
One other interesting pattern I'd like to bring up is the one that happens if you darken only the odd-numbered cells in Pascal's Triangle. You get a fractal pattern known as the Sierpinski Sieve. No, this won't tell you too much about the 12 days of Christmas, except maybe the occurrences of the odd days, but it can make a beautiful and original Christmas ornament! If you have kids who ask about it, you can always give them the book The Number Devil, which describes both Pascal's Triangle and Sierpinski Sieve, among other mathematical concepts, in a very kid-friendly way.
There's another 12 Days of Christmas calculation that's far more traditional: How much would the 12 gifts actually cost if you bought them? PNC has been doing their famous Christmas Price Index since 1986, and has announced their results. Rather than repeat it here, check out their site and help them find all 12 gifts, so that you can some holiday fun and then find out the total!
Since my Christmas spending is winding up, I'm going to have to forgo the expensive version, in favor of Miss Cellania's internet-style version of The 12 Days of Christmas. Happy Holidays!

 I apologize for the irregular posting over the past few months. I've had to deal with some personal issues (don't worry, everything is fine!). The good news is that, with this entry, everything should start returning to normal.
I apologize for the irregular posting over the past few months. I've had to deal with some personal issues (don't worry, everything is fine!). The good news is that, with this entry, everything should start returning to normal.

 I recently ran across a number of videos I figured would be interesting to regular Grey Matters readers, so I thought I would share them.
I recently ran across a number of videos I figured would be interesting to regular Grey Matters readers, so I thought I would share them.



 Would you believe tha another of my contributions has made it on to Scam School again? It was
Would you believe tha another of my contributions has made it on to Scam School again? It was 








 I apologize for not posting the past 2 Sundays, but my internet connection was down.
I apologize for not posting the past 2 Sundays, but my internet connection was down.




