Grey Matters favorite Werner Miller is back, and he's brought more of his amazing mathematical wizardry with him!

If you're not already familiar with him, he's a retired mathematics teacher in Germany who has created some of the most original and compelling magic routines I've ever come across. He is the author of several magic books, including Ear-Marked, which is available in the Grey Matters store.

Starting off, we have a couple of good routines that are perfect as promotional tools, since you can print them on your business cards or brochures, and have people perform them for themselves or others without understanding how they work. There's Vive Le Roi!, which includes several variations of routines where you move your finger from card to card, eventually winding up on a predicted card. You can have two people do this together, as they'll be on different cards until the last card.

The other trick along this line is Magic Patchwork, a similar trick with a magic square. He mentions that it was inspired by Pedro Alegria’s El cuadro de colores, but the link given is no longer functioning. Fortunately, it was captured by the web archive. The original is here, with a translation to English via Google Translate available here.

Werner Miller also created a very sneaky calculator trick, called You Push the Button... that seems to be a mathematical trick, but isn't. The use of the calculator helps conceal the outright sneaky method.

Getting back to his specialty of mathematical magic, he offers a great routine with dice. It's called Lined Up, and has two different phases, both of which begin with different-colored dice arranged with the numbers 1 through 6 in numerical order. In Phase 1, you have someone choose a die and turn that number face down. After getting the new total of these dice, you announce which color die has been turned over. Phase 2 is similar, except that you have someone choose a die and turn over every die EXCEPT for the chosen one!

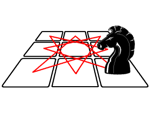
I've saved my favorite for last! It's called Ghost Rider, and uses a chess knight and some file cards. One of the file cards is signed, then mixed into the pile and dealt out into a 3 by 3 square. The spectator then uses the knight and their own free choices to find their own signed card! Part of the principle is taught here on Grey Matters in my Knight Shift post, as mentioned generously in Werner Miller's article. His added touches, however, make this a very impressive trick.

If you like Werner Miller's style and would like to see more, check out the rest of Werner Miller's work here on Grey Matters!

If I asked you to imagine a mathematical card trick, you'd probably picture some monstrosity such as the old 21-card trick.

However, mathematics isn't just about numbers, it's about patterns. This week, Scam School taught a 5-person mind-reading trick that demonstrates this point dramatically.

The trick in the following video is so amazing, one of the spectators refers to it as a Criss Angel-type trick. First, let's watch and learn the trick itself:



Brian gives a good explanation of the trick itself, but it's still not easy to see why the trick itself works. Fortunately, our old friend James Grime had previously posted a video on this same trick. This is a very clear explanation, aided by the use of different colored sheets to stand in for the separate cards:



In a trick like this, it's very important to understand the underlying principle clearly. This way, you're can allow the cards to be handled more freely while still understanding what types of mixing will ruin the trick, and what types won't affect the stack. For example, when Brian Brushwood took the cards back, he made sure to reverse each person's individual pile, but in a manner that made it seem like random mixing.

Notice that Brian keeps the focus on poker terminology, outright referring to each of the piles as hands. This is excellent psychology, as it helps put your audience in a mindset that you're some sort of master poker cheat with a penchant for telling on which cards people focus.

As I mentioned earlier, this is a mathematical card trick, not in the number sense, but rather in the sense that you're taking advantage of a simple pattern. In fact, the pattern is so simple, that's why putting the focus elsewhere, such as on a poker theme, is important.

This type of simplicity, as I've discussed before, is often difficult to achieve. When it's achieved, though, the results are rarely less than remarkable.

The holy grail of memory is considered to be eidetic memory, what is more commonly as known as a photographic memory.

Currently, there's plenty of skepticism about it. That's largely because there's so little scientific study about it, coupled with the rarity of finding anyone who truly has it. Fortunately, that's all starting to change.

If you've spent more than 5 minutes reading Grey Matters, you realize that there are many clever ways to simulate a great memory, and even to use a trained memory to appear to be far better than the true credit it deserves.

We'll start with a 2010 National Geographic story about Gianni Golfera. He's being studied by researchers because of his extraordinary memory abilities. However, he has also learned, created, and taught memory systems that anyone can use, so there's a question of just how much of his memory is due to biology and how much is due to practice and determination.



More recently, it's been discovered that there is a specific type of enhanced memory, called “hyperthymestic syndrome”, or less technically, “superior autobiographical memory”, that may be at the heart of this unusual phenomena. I mentioned this briefly back in 2008 on my post about Jill Price.

In that same post, I also mentioned that Taxi star Marilu Henner is also hyperthymestic. Late last year, she appeared in a 60 Minutes report about superior autobiographical memory with some others with the same condition.

This is worth watching, because it's a more detailed account of the condition, the people who have it, and the state of the current research about this little-understood phenomenon:

Last week I introduced the updated version of Verbatim. It's a free web app to help you with memorization that doesn't require any registration.

Are there any other such web apps? Yes, and we'll cover many of them in this post.

While all the web apps below can be used without registration, some of them do offer extra functionality if you do register. In those cases, registration itself is also free.

• Pinfruit: If you're familiar with the Peg/Major System, as described in Pinfruit's own user guide and in Grey Matters' Memory Basics post, then you'll find this web app to be a handy tool. It helps you remember numbers by translating them into words using the Peg/Major system.

• MemorizeNow: Out of all the web apps on this list, this is probably the closest to Verbatim. You paste in the text you wish to remember, save it, and you're quizzed by either first letters or a fill-in-the-blank quiz. The video below shows you Memorize Now in more detail:




• Think-A-Link: This may not be as interactive as many of the other web apps here, but is hard to pass over when talking about memory. This site has many fun and original links for just about every subject you can think of, and even a few that you can't. The best links from this site have even been collected in the book, Think of a Link.:




• JogLab: JogLab focuses on help you remember lists with acrostic mnemonics. Acrostic mnemonics are those where you remember a silly phrase or poem to remember another set of information, such as “Richard of York gave battle in vain” for the colors of the rainbow, or “Every good boy does fine” for the remembering the notes for the main lines of the treble clef in music. JobLab helps you develop your own mnemonics with a very simple interface:




• Verbatim 2: OK, forgive the shameless plug, but I couldn't resist adding my own program to the list for those who don't already know about it. Verbatim is a web app for memorizing text, similar to MemorizeNow above, but takes a different and more detailed approach:




Don't forget, too, that these and many other fine memory tools are always available by clicking the MEMORY TOOLS button at the top bar of any page on Grey Matters.

Over in the Mental Gym, there's a tutorial all about the unit circle, which I published back in February. It focuses mainly on radians, Pi, sine and cosine.

I've had a few e-mails asking how to understand the other trigonometric functions: tangent, cotangent, secant, and cosecant. As of today, that new tutorial is up - Unit Circle 2: Trig Functions.

As suggested on the first page of the new tutorial, you should read and understand the original unit circle tutorial first.

In high school trigonometry, most people are told they'll really only need to know about sine and cosine, and a little bit about tangent. The formulas are explained, but never really their nature. It's one thing to be able to get the answer, and quite another to understand what the answer means.

My goal in the new tutorial was to be clear about the whats and whys of the other trig functions. You may never use them, but if you understand them, you'll quickly recognize when you can potentially use them.

Once you understand what each function covers, I lock in the important points of each function with mnemonics. Sure, you've probably run across SOHCAHTOA, but I've got a less familiar mnemonic covering all 6 functions that will have you saying “OOH! AAH!”.

Thanks to my recent experiences with Wolfram|Alpha, links to their knowledge engine were used in several examples. I only wish I'd known about Wolfram|Alpha sooner!

Considering the number of books and articles through which I had to look to develop these descriptions, I do believe that this new tutorial presents tangents, cotangents, secants, and cosecants in a way that's among the clearest out there.

If you have any further suggestions about the clarity of this tutorial (or anything else on Grey Matters), or have any questions about something that could be presented more clearly, let me know in the comments!

2 years ago, I released a free iPhone/iPod Touch web app called Verbatim, which was designed to help you memorize texts of any lengths word-for-word, such as monologues, poems, presentations, scripture, scripts, song lyrics, and speeches.

After hearing the feedback to the previous version, today I'm announcing the release of Verbatim 2.0! Yes, it's still free. Now it's easier than ever to use, and available for a wider array of mobile devices.

Verbatim was inspired by J. J. Hayes' post, How To Memorize A Poem. It's a brief article, but the I've found the technique to be very effective.

The most frequent complaint about the previous version was the requirement that a custom file had to be prepared and hosted remotely for it to work. In the new version, I've done away with that completely. Now, entering the piece is as simple as cutting and pasting.

The need to access the remote file also created a second obstacle, you had to have an online connection for it to work. Thanks to the new method of entering the text, as well as a few other programming techniqes, Verbatim 2 is completely self-contained and can now be used offline! It never needs to access any other files from anywhere, and only requires online access if you desire to visit the links in the manual.

The simplest way to use Verbatim offline is to download it from the above link, put it in your Dropbox account, sync up your mobile device's Dropbox app, and then run Verbatim in the app. I've only tried this myself in iOS devices, but it should work in a wide variety of mobile devices.

The following video will give you a more complete look at the updated version of Verbatim:



You can download an MPEG4 version of this video for offline viewing at: http://tinyurl.com/v2video

Verbatim was completely re-written in jQuery Mobile 1.0 beta 1, so that a wider array of mobile devices and desktops could run it. Many of the supported platforms are mentioned in the video tutorial above, and in the manual, with more detailed information available about supported platforms here.

If you're inspired to start memorizing a piece of text, there's plenty of good starting points in the related resources page of the manual. There's also many good poetry posts right here on Grey Matters. I've tried to cover different styles, from classic to modern to funny, and just downright bizarre.

I'd love to hear if Verbatim helps you, as well as answer any questions, problems, and suggestions in the comments.

July's snippets are here, and they're full of free mathematical goodies!

• Marcus du Sautoy, whom you may remember from his BBC series, The Story of Maths, has definitely been keeping busy. Besides that documentary, you can find his 10-part podcast series A Brief History of Mathematics available for free via the BBC (or, strangely, as an audiobook for sale). This is a great introduction to the giants of mathematical history.

You can also see him lecture for free about symmetry on TED, or about prime numbers at Hebrew University (via YouTube).

• I've talked about game theory recently, yet I only recently ran across a great tool for studying it. Gambit is a free game theory analysis program that runs on Windows, OS X, and Linux. There are two excellent and simple tutorials available on the site (available as both Flash movies and PDF documents) to get you started. It makes a wonderful companion tool to game theory courses, such as Game Theory 101 (free via YouTube), Ben Polak's Game Theory course at Yale (free via Yale, YouTube, or iTunes, course documents available at Yale link). I first learned about this while watching The Teaching Company's game theory course, Games People Play, which is also an excellent introduction to the field.

• Speaking of unusual calculators, iOS mobile device users should check out the free Magical Calculator app. Instead of just being a standard calculator app, you can prepare it with your own custom formulas and inputs (such as those for interest on loans or physics equations), and then you'll always have your own handy custom calculator ready! If you're familiar with InstaCalc website from BetterExplained, this is basically the same idea turned into an app.

Speaking of freebies, I'll have a very special one (non-mathematical) for you in Thursday's post!

Ever do one of those tricks where you have someone pick a number, and have them do things like add 5, double it, subtract 4, divide by 2, subtract their original number, and you determine that the answer they got was 3?

As many people realize when you're doing such a trick, the whole process boils down to an algebraic formula that applies to any number. Today, we're going to turn that process on its head by figuring out a formula secretly chosen by your audience!

After being shown the following math trick by W. W. Sawyer, Martin Gardner wrote it up in his books, New Mathematical Diversions and The Colossal Book of Mathematics.

Here's the original write-up, in Martin Gardner's words:

Instead of asking someone to “think of a number” you ask him to “think of a formula.” To make the trick easy, it should be a quadratic formula (a formula containing no powers of x greater than x²). Suppose that he thinks of 5x² + 3x - 7. While your back is turned so that you cannot see his calculations, ask him to subtitute 0, 1, and 2 for x, then tell you the three values that result for the entire expression. The values he gives you are -7, 1, 19. After a bit of scribbling (with practice you can do it in your head) you tell him the original formula!

The method is simple. Jot down in a row the value he gives to you. In a row beneath write the differences between adjacent pairs of numbers, always subtracting the number on the left from its neighbor on the right. In a third row put the difference between the numbers above it. The chart will look like this:



The coefficient of x², in the thought-of formula, is always half the bottom number of the chart. The coefficient of x is obtained by taking half the bottom number from the first number of the middle row. And the constant in the formula is simply the first number of the top row.

(NOTE: Check out the other posts in The Secrets of Nim series.)

We're going to continue the discussion of the game 31 from the previous post, so make sure you've read that post first!

Just so we have them handy in this post, we'll go over the winning strategies for 31 once again:

• Ask yourself: “Can I rotate the die so as to get to a running total with a digital root of 4 (4, 13, 22, or 31)?” If so, do it! If not...
• ...Ask yourself, “Could I rotate the die to a 3 or a 4, so as to get to a running total with a digital root of 1, 5, or 9 (1, 5, 9, 10, 14, 18, 19, 23, 27, or 28)?” If so, do it! If not...
• ...rotate the die to a 2 or a 5, so as to obtain a running total with a digital root of 8 (8, 17, or 26). Assuming the other player hasn't purposely or accidentally made a good move, this one will still be possible.