 I finished the previous post about Prime Test and Pascal's Triangle by mentioning that exploring one idea can often take you to some surprising places.
I finished the previous post about Prime Test and Pascal's Triangle by mentioning that exploring one idea can often take you to some surprising places.
Exploring those same idea even further, I've run across some additional surprising ideas that I'll share in this post.
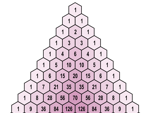
• SIMPLIFYING THE TEST: I finished the Pascal's Triangle exploration of the AKS test by mentioning that, if the test returned a row of all zeros, as in this test run on 71, then the given number n is prime.
After seeing this picture, linked from this thread on Reddit, which used the idea of summing (represented by the ∑ symbol) the results of each iteration, I smacked myself in the head for not thinking of that before. Here's the test for 71 re-run with summation. It's certainly much easier to see whether the total is 0 or not.
• FINDING AN ERROR: I thought it might be fun to see how this function looked on a graph, so I headed over to the Desmos.com online graphing calculator. Unfortunately, it didn't work because their software seems to have some sort of bug which occurs when binomials are run through modular arithmetic.
For example, it calculates 462 mod 11 correctly, but when a binomial is calculated as 462, and that binomial is calculated mod 11, then the odd result of 11 occurs (the answer should be 0). I even found another example, where mod returns an answer that isn't even a whole number!
I posted about this bug to Desmos on Twitter, here and here. They've already replied and will have their programmers look into the problem.
• EASIER PEASIER BINOMIAL EXPANSION: I guess the easiest version of binomial expansion would have to be this picture, but there's a more mathematically correct approach that's also quite easy.
Steven Pomeroy of mathtricks.org teaches a great way of expanding binomial equations, even when Pascal's Triangle isn't handy! If you're interested in just the coefficients, as we were in the AKS primality test, you can even skip down to about half way, where he teaches how to calculate each coefficient in the row.
I've found a way to simplify Mr. Pomeroy's version of the calculation that works better for me, so I'd like to share it with you. Recall that the 0th binomial, the leftmost number on any row of Pascal's Triangle, is always 1, so we always start this with 1.
First, you need a row, so we'll use row 8 as an example. You start by creating a fraction with the row number on top, and a 1 on the bottom. In our 8 example, the first fraction would 8⁄1. We'll also be using subsequent fractions in further calculations, which will decrease the numerator (the top number) by 1, while increasing the denominator (the bottom number) by 1. So, the sequence of calculations for row 8 would run as follows:
8⁄1, 7⁄2, 6⁄3, 5⁄4, 4⁄5, 3⁄6, 2⁄7, 1⁄8
That sequence should be easy enough to understand. Also, note that the last half of that fraction sequence are simply reciprocals of fractions in the first half, so the resulting answer we get when multiplying by these fractions will rise and fall symmetrically, as we discussed in the previous post. So, the only part of the fraction sequence you really need from above are those where the numerator is greater than or equal to (in the case of odd numbered rows) the denominator:
8⁄1, 7⁄2, 6⁄3, 5⁄4
After that, the row goes down with the numbers in the same order, due to the symmetry of Pascal's Triangle.
What do we do with these fractions? You're going to multiply them by whole numbers, record the answer, and then use that answer to multiply by the next fraction in the sequence. This may sound confusing, so I'll return to our example using 8.
We always start with 1, and multiply it by the first fraction, which is 8⁄1 in this example. 1 × 8⁄1 = 8, so we have our first two numbers in the sequence:
1, 8
Next, we adjust the fraction as described above (decrease numerator by 1, increase denominator by 1), and multiply it by our new answer. 8 was our previous answer, and 7⁄2 is the next fraction, and 8 × 7⁄2 = 28. We already have 3 terms in the sequence:
1, 8, 28
We continue on, each time using the previous answer multiplied by the next fraction in the sequence. 28 × 6⁄3 = 56, and 56 × 5⁄4 = 70, giving us:
1, 8, 28, 56, 70
Since the next fraction would be a reciprocal of 5⁄4, we know that the numbers are going to start decreasing in the same way they increased, so we can just fill out the remaining half symmetrically:
1, 8, 28, 56, 70, 56, 28, 8, 1
Sure enough, that's exactly how the 8th row of Pascal's Triangle appears!
With 9, or any other odd row, you're going to multiply by the following fractions, until you get down to the point where the numerator and denominator are the same:
9⁄1, 8⁄2, 7⁄3, 6⁄4, 5⁄5
As before, we start with 1, so 1 × 9⁄1 = 9, 9 × 8⁄2 = 36, 36 × 7⁄3 = 84, 84 × 6⁄4 = 126, and 126 × 5⁄5 = 126, giving us the following sequence of numbers:
1, 9, 36, 84, 126, 126
Obviously, it's time to apply the numbers to the end symmetrically, giving us this sequence, which is how the 9th row of Pascal's Triangle appears:
1, 9, 36, 84, 126, 126, 84, 36, 9, 1
Multiplying by weird fractions like this might seem intimidation, but it's actually easier than it seems. When given ANY fraction, even an improper fraction (one where the numerator, the top number, is greater than the denominator, the bottom number), think of the numerator as the number by which to multiply, and the denominator as the number by which to divide. You can do the multiplication and division needed in either order, as well!
Let's take what is possible the worst example from above, which would be 36 × 7⁄3. The numerator is 7 and the denominator is 3, so you could multiply 36 by 7, getting 252, and then dividing that by 3 to get 84. However, in this particular example, it seems easier to divide 36 by 3 first, to get 12, and then multiply that by 7 to get 84. See how easy it is when you know how?
That's all for this post, but that's also plenty to explore, practice, and enjoy!

 "Problems worthy of attack prove their worth by hitting back." - Piet Hein, "Problems"
"Problems worthy of attack prove their worth by hitting back." - Piet Hein, "Problems"