Here in the US, where we use a month-day-year order, today is 10-11-12 for short.

I thought I'd take advantage of this unusual date sequence to take a look at the amazing power of some other mathematical sequences.

If I handed you 13 cards of different values, the simplest sequence would be to put them in Ace through King order. What if I challenged you to put them in a sequence such that when you spell the word Ace, you get the the Ace, then spell the word two, and you get a two, and so on? That's the basic trick taught in the following video:



How is this done? Here's the explanation video.

How did anyone come up with this sequence in the first place? That's actually very simple. Take out 13 cards of all the same suit, and put them face-down in Ace through King order, with the Ace as the top card, and the King as the bottom card (if the cards were turned face-up, you'd be looking at the King).

Next, spell Ace by putting one card for each letter on the bottom, then taking the next card, just as in the above video. Since you've ducked 3 cards and removed the 4th, this will naturally be a 4 of whatever suit you removed. This means that the Ace should be the 4th card in the sequence. Continuing with spelling t-w-o, you'll turn up an 8 next, meaning that the 2 should be placed as the 8th card.

Doing this all the way up through spelling k-i-n-g, the order you'll get will be 4-8-A(1)-7-K(13)-6-3-2-Q(12)-J(11)-9-5-10. Note that in the explanation video, note that the Ace is the 4th card, the 2 is the 8th card, the 3 is the first card, and so on. If you ever forget the sequence as taught in the video, now you know how to work this out.

Let's take this sequence to the next level. In the book Scarne on Card Tricks, there's a version of this trick called “The Uninvited Joker”, which can be learned online (part 1, part 2). One performing tip I'd add from experience: If you switch the roles so that the spectator successfully spells the card, and you (the performer) keeps getting the joker, the audience is put more at ease, and is more likely to be entertained.

Another simple, yet amazing, sequence took the internet by storm earlier this year was the fact that 1/998001 = 0.000001002003004...996997999000001.... In other words, the decimal representation is a sequence of almost every number from 000 up to 999 before repeating. Naturally, James Grime couldn't resist making a Numberphile video about it:



As you can see, even simple sequences can have amazing and surprising results. As recently as the previous post on the Latin ESP Square, you can see evidence of just that. There are numerous amazing sequence to explore here on Grey Matters, including the Fibonacci sequence, de Bruijn sequences, the Gilbreath Principle, the Kruskal Count (part 1, part 2), and even Penney's sequences.

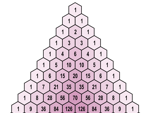
How do we wind up this discussion of sequences? The only possible way is with a sequence of sequences! The always amazing Pascal's triangle, as seen in the presentation below, only scratches the surface of its amazing qualities:



In my 12 Days of Christmas post, I talk about many of the other aspects of Pascal's triangle, including the fact that you can get a Sierpinski triangle by differentiating odd and even numbers, as demonstrated here on Wolfram Alpha. Try it modulo 3, modulo 4, and so on (try clicking the More Rows button) to see even more impressive patterns.

Have fun exploring these amazing sequences!