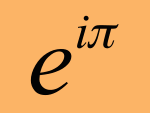Today, I'm going to take you on a journey. It's a sort of imaginary journey, but not in the way that you may think.

This is a mathematical journey, and if you can grasp where we start, I think you'll enjoy where we wind up.

There are two important concepts with which you'll need to be familiar before we begin. The first is the idea of imaginary and complex numbers, which are explained intuitively in A Visual, Intuitive Guide to Imaginary Numbers. The other concept is the number e, as explained in An Intuitive Guide To Exponential Functions & e. Take your time, if needed, to understand these concepts, and the rest of this post will be well worth the time spent.

We'll start simply, with a right triangle that's half as high as it is long (via Desmos.com). The coordinates of the vertices in Cartesian coordinates are (0,0), (1,0), and (1, 0.5). Converting these to complex numbers, they respectively become as 0 (0 + 0i), 1 (1 + 0i), and 1 + 0.5i. As you can see, converting between complex numbers and Cartesian coordinates requires little effort.

Just for fun, let's see what happens if we take this 1 + 0.5i right triangle, and take it the integer powers from 1 to 10. Wolfram|Alpha calculates the answers to (1 + 0.5i)ⁿ quickly, for values of n from 1 to 10, but the answers are just complex numbers, with no real apparent meaning.

Desmos.com can't handle complex numbers, but can handle tables of Cartesian coordinates, so if we use those answers, and draw the corresponding triangles, we get a very visual interpretation of these complex numbers!



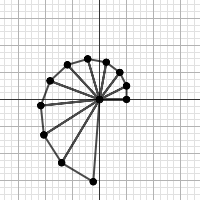
What we get is a series of larger and larger right triangles! Think about why this is, using our old friend, the Pythagorean theorem. The horizontal leg is 1 unit, the vertical leg is 0.5 units, so the Pythagorean theorem tells us that the hypotenuse of that first triangle is about 1.11803 units long. That's also the base of the next right triangle.

The distance formula can be used to work out the height of the new triangle. It starts at (1, 0.5) and ends at (0.75, 1), so we plug the numbers in to get d = √(0.75 - 1)² + (1 - 0.5)² = √(-0.25)² + (0.5)² = √0.0625 + 0.25 = √0.3125 ≈ 0.559017.

Notice that, if you double 0.559017, you get 1.11803. That's not a coincidence. What you're getting is a series of triangles with progressively longer legs, and whose heights will always be half of that length. In short, (1 + 0.5i)ⁿ builds n right triangles with a 1:0.5 (or 2:1) ratio for the legs, and hypotenuses who lengths grow in accordance with the Pythagorean theorem!

Now, the formula (1 + 0.5i)ⁿ looks a little like the part of the formula for e. What would happen if we changed it to (1 + ^0.5i⁄_n)ⁿ? Let's look at this step by step.

With just 1 power, and therefore just 1 triangle, the formula gives us 1 + 0.5i, not surprisingly. This gives us our original right triangle.

Next, let's change the power to 2, and step through the formula twice to get 2 triangles. Wolfram|Alpha returns 1+0.25i and 0.9375+0.5i. We still get 2 triangles, but now they occupy about the same height as the previous single triangle!



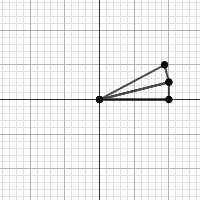
Sure enough, if we take 3 steps through the 3rd power, we get 3 right triangles with about the same total height as the others.



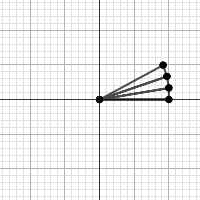
This should make sense, especially as this approach was inspired by e. Remember how the change in e gets smaller and smaller as bigger numbers are used for n? Just like e packs smaller and smaller numbers in the same numeric space, our right triangles are packing more and more triangles in the same space on the graph!

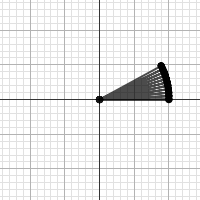
Yes, if we take this approach to the 10th power and take 10 steps through it, we get 10 right triangles packed into the same space.



Let's take a closer comparison of this formula to e. First, the actual definition of e is:



We didn't take that limit into consideration in our triangle demonstration. What happens as our number of triangles get closer and closer to infinity? There will be more and more, so the height will get closer and closer to 0 units. If the height gets closer to 0, the Pythagorean theorem tells use that the hypotenuse will get closer and closer to the length of the original leg, which is 1 unit.

If you can picture infinitely many triangles packed into that same space, you can see that it would almost be like the lengths of the long legs would all be 1 unit, so it would effectively be a perfect arc!

The more general definition of e defines what happens when e is taken to a power:



So, if we apply that limit to our original complex equation, (1 + ^0.5i⁄_n)ⁿ, that means the infinitely many right triangles yields the same result as e^0.5i! Remember that taking our formula to the 10th power ended in 0.888809+0.485079i, so you shouldn't be surprised to see that e^0.5i roughly equals 0.877583 + 0.479426i.

Wolfram|Alpha's Arg[] command takes a complex number and returns the equivalent in radians. Entering Arg[0.877583 + 0.479426i] gives us the rather interesting result of 0.5 radians!

Let's think about this. Plotting out an infinite number of triangles of the form (1 + ^0.5i⁄_n)ⁿ, the equivalent of e^0.5i, results in an arc that's 0.5 radians long.

Yep, we're actually getting visual and mathematical proof that e^ix will result in an arc that's x radians long! If you understand trigonometry, this means you can use sine and cosine to work out the same point calculated by e^ix, which is exactly what Euler's formula says!

Yep, since Pi radians is half a circle, then our formula becomes e^iπ, which is Euler's famous identity! Since the cosine of π = -1 and the sine of π = 0, it works out -1 + 0i, or simply -1.

Did you ever think that playing around with a few triangles would ever lead you to an understanding of e^iπ = -1?