John Conway has brought many new mathematical recreations to the general public. Martin Gardner wrote about him quite often in his Scientific American columns, and I've referred to his works many times here on Grey Matters.

Today's post focuses on a puzzle Conway created. It uses 4 people, some ropes, and is referred to as Rational Tangles, or just Tangles, for short.

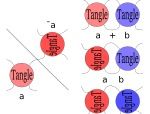
Imagine 4 people standing as if they were at the 4 points of a square. In the diagram below, each colored dot represents a distinct person:



Next, 2 ropes are handed out. One of the ropes is held by Blue at one end, and Red at the other end. The other rope is held by Green at one end, and Black on the other end, like this:



In reality, both ropes would be the same color. 2 different color ropes are only used here to make things clearer. Later on, I'll be referring to the above illustration as the starting position. Now that we have the basic set-up, it's time to introduce the rules of the puzzle.

From this point, there are only two moves allowed. The first is a simple 90° clockwise rotation, as seen from above, of all players. This move is referred to as a rotation. From the starting position (above), a clockwise rotation would end with the players and ropes in this position:



The only other legal move, known as a tangle, is performed by having the players in the upper right and lower right (again, as seen from above), switch places. As this happens, the player in the upper right lifts up their rope, and the player in the lower right goes underneath. Not surprisingly, this results in a crossing of the ropes.

Going back to our original starting position, with Red in the upper right and Black in the lower right, a call for a twist would start with Red holding its end up while heading to the lower right, and Black going underneath Red's rope, while heading for the upper right. At completion, the result would appear like this (again, remember this is starting from the original starting position, NOT the previous illustration):



The idea is that you have the 4 people involved, and/or anyone else who is watching to call out a long combination of tangles and rotations, in order to ensure that the 2 ropes are well intertwined. The challenge is, with the tangled section of the rope hidden from view, to untangle the ropes once again.

You might think the solution would simply be to use a memory system to memorize all the calls made, and then call them out in reverse order, making sure you untwist and unrotate at the appropriate steps. The problem here is that untwists and unrotations aren't legal moves.

The only moves you can use, remember, are a 90° clockwise rotation, and a switching of the two rightmost people, such that the rope of the upper right person goes over the rope held by the lower right person as they switch.

Using only those two moves, is it always possible to return to an untangled state? Surprisingly, the answer is yes. The question of course, is how do you do it?

The answer involves keeping track of the tangles mathematically. As there are only two types of moves, this is easier than it might sound. However, the mathematics do involves working with fractions. Should you need a refresher course on fractions, I recommend starting with Math Dude's series of podcasts on fractions (starting with the Nov. 16, 2012 episode). WhyU's video series on fractions, mainly from episode 12 to episode 17, are also very helpful. You'll also want to make sure you're comfortable adding and subtracting negative fractions with a common denominator.

Yes, I know the mentions of fractions, which many math students consider the real F-word, makes this sound scary, but once you get used to the process, it's not as bad as it may seem at first.

Getting back to Conway's Tangles, James Tanton's Rational Tangles PDF is the easiest introduction to the mathematics behind this puzzle.

If you're viewing this on a device that supports the Flash plug-in, NRich.maths.org has some wonderful tools to help you understand Conway's Rational Tangles, as well.

Not surprisingly, you're going to get the best understanding of Rational Tangles from the inventor himself. I'll wind this post up with John Conway's full, 74-minute Tangles, Bangles, and Knots lecture, courtesy of UCTV Prime: