 Today is 6/28, making it Tau Day! Tau is a constant equal to 2 * Pi.
Today is 6/28, making it Tau Day! Tau is a constant equal to 2 * Pi.
It sounds simple, and suggests that Tau shouldn't be a big deal. However, there is an entire movement to have Tau take Pi's place!
Let's start with good old familiar Pi (π). The following video, The Story of Pi, is a great refresher course on a very useful constant:
One of the most useful places for Pi is throughout the unit circle. If you need a refresher, here's a clear and simple Unit Circle tutorial.
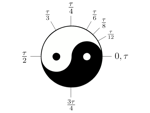
With those concepts in mind, let's have Vi Hart explain why Tau (τ) is a better alternative to Pi.
There's plenty of support for Tau. Dr. Kevin Houston has another excellent intro to Tau, and Vi Hart even recently released a Tau Day song.
Michael Hartl, who began the Tau movement, offers a much deeper look at the effects of Tau in a 51-minute lecture, as part of his full Tau Day website. The Tau Manifesto itself is also available on the site for free.
Bob Palais classic article π is Wrong! (PDF link) is also considered to be a must-read for Tau enthusiasts.
Much of that was around for Tau Day 2011, however. This year, however, Tau faces an entirely new challenge!
The new challenger is Eta (η), which is ½π, effectively the inverse of Tau. David Butler's video shows the surprising uses of Eta, some of which rival Tau AND Pi!
That only leaves us π Day being on March 14th (3/14) and τ Day being on June 28 (6/28) is well and good, but when would we celebrate η Day? January 57th? Perhaps February 26th?
Why are we looking solely at the constant for change? How about changing the measuring unit? Since π is defined as a circle's circumference to its diameter, why not measure the circle in diameter lengths instead of radius lengths?
We could call these units “diameterians”, which would be equal to 2 radians. A complete circle would have π diameterians.
Notice that even from the seemingly simple shape of a circle, we can look at it from so many different ways. That's been part of the fun of putting up this post.
What do you think is the way to go? π? τ? η Diameterians? I'd love to hear your thoughts in the comments!
7
Pi vs. Tau vs. Eta
Published on Thursday, June 28, 2012 in controversy, fun, math, Pi, self improvement, videos
Related Posts
Post Details
Subscribe to:
Post Comments (Atom)




7 Response to Pi vs. Tau vs. Eta
Pi. This whole pi vs. tau thing is nonsense and eta is just adding fuel to the fire. It's really not a big deal. I also love how pi reflects the long history of mathematics. We use circumference/diameter and not circumference/radius because with primitive tools it was so much easier to measure the diameter of a circle than the radius. These roots are everywhere. Like geometry, which literally means 'land measurement,' shows how today's complex math comes from Greek farmers trying to plot out fields efficiently. Keep it pi.
I find this discussion to be utterly fascinating! I think everyone is right! Obviously, as a practical matter, for historical reasons as well as intellectual inertia and with hints of the qwerty phenomenon at work, pi is the clear winner and will be with us for quite a long time to come. After all, although the Good Lord may not play dice, God definitely ratified the choice of pi by having Albert Einstein himself born on Pi Day, March 14, 1879, a Friday! Vi Hart, the wonderful and precocious niece of one of my best friends Kathleen, makes a very persuasive case for tau = 2*pi and there are, indeed, far too many fundamentally important equations in physics and math that are littered with ungainly factors of 2*pi--for example, Euler's beautiful formula for the Euler-Riemann zeta function for any positive even number 2*n: zeta(2*n) = [(-1)^(n+1)]*{B_2*n}*[(2*pi)^(2*n)]/2/[(2*n)!], where B_2*n is a Bernoulli number! However, as a purely logical matter, I have to admit that David Butler's arguments for eta = pi/2 are the most persuasive! Personally, given my last name (Furlong), which is defined to be 1/8 of a mile and is most often encountered in horse racing, I think that kappa = tau/8 = pi/4 = eta/2 = 0.7853398163397448... would be another fine choice for a fundamental transcendental constant number if for no other reason than that kappa is the first Greek letter in the Greek word for a circle, kuklos! Upon Latinization, the Greek upsilon becomes the English "y" so that the etymology of "cycle" from kuklos is readily seen! Also, kappa is usefully a real number betweem 0 and 1, for whatever that's worth! Trigonometrically, sin(kappa) = cos(kappa), uniquely, and kappa is the unique angle any diagonal of a square makes with the sides of the square! Notwithstanding all the enchanting and intriguing arguments for tau and eta and kappa, I stay with the observation I started with, namely, that pi is here to stay supreme for quite a while, which makes my successful efforts at committing the first 1512 decimal digits of pi to memory seem slightly less ridiculous than they were! Why did I stop at 1512? Well, 1511 is the 240th prime number, there are 24 hours in a day, and 10 is the well-known and well-beloved base of our decimal system, and I couldn't properly round pi to 1511 decimal places without knowing the value of the 1512th decimal digit (which happens to be a 7, coincidentally the lucky number of days in a week, which causes the 1511th decimal digit, 8, to round up to 9, which also happens to be the 1510th decimal digit!)--the real reason is that I eventually became somewhat bored with the whole project, which was taking up too much time every day since I tended to remember all 1512 numbers better if I recited them in my head in conveniently bite-sized groups of 10 daily! Clearly, I also desperately needed to get a life!
Definitely Tau. Because the number in front of Tau is equivalent to the portion of a circle traversed, it makes the geometrical meaning of equations so much clearer. E.g. A=1/2 tau r^2 might seem less clear but even there in the equation is a hint at the proof. Likewise e^i tau = 1 makes sense because an entire turn leaves you where you are. But it'll probably never change, so pi'll have to do
"Diameterans" don't work. All the things like the derivative of sin being cos, the infinite series for sin, cos, and arctan, etc. only work with radians. The whole point of radians was to have a natural, elegant unit rather than an arbitrary one like degrees, but diameterans would be just as bad as degrees. That's basically the problem with pi; the Greeks didn't have radians so they arbitrarily decided to look at the diameter instead, but now that we have radians, pi messes things up with a factor of 2. So pi is really just a historical mistake, and it wouldn't be so difficult to fix this mistake if it weren't for people trying to make excuses for pi like saying "it doesn't matter" (interestingly, I find that most people who say this are pi supporters just using it as a reason to still use pi when it is clearly inelegant and not bringing anything new to the debate). If you have nothing to say other than "it doesn't matter," why do you care enough to even comment on the debate? It's pretty obvious that the real reason is just that those people refuse to change the status quo.
To the first commenter here:
Saying "pi reflects the long history of mathematics" is an argument from tradition. You even mentioned that the only reason we used it was because of primitive measuring tools, which isn't a good reason at all. Should we still use degrees instead of radians and Roman numerals instead of base 10 just because they "reflect the long history of mathematics"? Of course not! Just because something has been used for a long time doesn't mean we should force ourselves to keep using it.
I think eta is really only useful when looking at right angles and not any other angles. David Butler's video showed the importance of right angles, but it also showed how confusing eta would be to teach beginning students when his first definition of it was the ratio of paths argument, which is not only an extremely confusing definition, but it also doesn't even work. Eta is only the ratio of paths when the long path is a semicircle; when it is any other arc, eta doesn't work, so eta doesn't describe a circle at all that way. The argument that you you can get the 4th roots of unity from Euler's identity with eta was also pretty bad considering that roots of unity are e^(iτk/n), so they are actually simpler with tau, and the 4th roots of unity really do just come from τ/4, not eta.
Randy it's interesting that you ended at 1512 and noted 1511 is the 240th prime number. While 1511 has nothing to do with Fibonacci numbers 240 is the product of 1,1,2,3,5,8, the first 6 non-zero digits of the Fibonacci sequence. Just saying.
Post a Comment