Back in the days of Ancient Greece, a mathematician named Eratosthenes managed to determine the approximate circumference of the Earth.

How did he do this? Even better, how could you go about repeating the experiment to teach the idea in modern times?

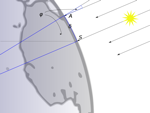
Let's start with the original experiment. Here's the story of Eratosthenes' experiment, as told by Charles and Ray Eames, whom you may know best from their education film, Powers of 10:



The actual angle measurement Eratosthenes got from the obelisk's shadow was 7°12', or 7.2°. Dividing 360° by 7.2° gives 50, meaning that 7.2° is 1/50th of the full circumference. That's why he multiplied the distance between the two towns by 50.

It's important to note that Eratosthenes was working longitudinally (running north/south). If the Earth were a perfect sphere (it isn't), the circumference would be the same all around. Since this experiment ran longitudinally, you get what is known as the polar circumference, as opposed to the equatorial circumference.

So, how close is the 25,000-mile measurement to the Earth's actual polar circumference? With modern equipment such as satellites, we've been able to determine that the Earth's average polar circumference is 24,818 miles - an accuracy of more than 99.27%!

How could you teach this with modern tools? There's a simple approach taught in this PDF that uses Google Earth. While you can't put a stick in the ground of Google Earth to measure a shadow, Google Earth already gives degrees of longitude. Thanks to that and Google Earth's ruler function for determining distance, this makes the virtual version of this experiment much easier to perform.

Of course, if the real Earth was good enough for Eratosthenes, why not use it today? In Eratosthenes' time, he had to wait an entire year before making the measurement back in Alexandria, so he could know that the Sun and the Earth were in the same relative position.

Modern communication makes it simple to arrange for the same experiments to be done at the same time on the same day in two different places. Rhett Allain of Southeastern Louisiana University and Chad Orzel of Union College in Schenectady, NY got together and did just this, as described in their respective links. They made time lapse videos, coordinating the times of their measurements, and posted their resulting time-lapse videos on YouTube: