April 10th is both the anniversary of Henry Ernest Dudeney's birth, as well as the anniversary of Sam Loyd's death. Henry Ernest Dudeney was to puzzles in England what Sam Loyd was to puzzles in America.
In honor of those anniversaries, I'd like to take a close look at a particular puzzle from Henry Dudeney's second book, Amusements in Mathematics (available online at Project Gutenberg for free), which he called the Four Frogs.
Henry Dudeney's presentation of this classic puzzle, dating back to 1512, included the following description and fanciful illustration:
341.—THE FOUR FROGS.
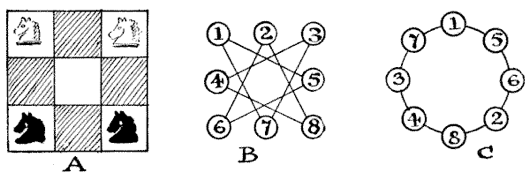
In the illustration we have eight toadstools, with white frogs on 1 and 3 and black frogs on 6 and 8. The puzzle is to move one frog at a time, in any order, along one of the straight lines from toadstool to toadstool, until they have exchanged places, the white frogs being left on 6 and 8 and the black ones on 1 and 3. If you use four counters on a simple diagram, you will find this quite easy, but it is a little more puzzling to do it in only seven plays, any number of successive moves by one frog counting as one play. Of course, more than one frog cannot be on a toadstool at the same time.
The original version of this puzzle employed a chessboard, two black knights, and two white knights. The way the frogs move along the lines in the above puzzle is based on the way a chess knight moves on a chess board: one square vertically and two squares horizontally, or one square horizontally and two squares vertically (as shown here).
It seems like a simple enough puzzle, but it's surprisingly challenging. Try it yourself below. That's not just an image, it's a working version of the puzzle. The object in the version below is to switch the positions of the black knights with those of the white knights (when completed, the board should look like this).
To move a knight, simply click on the knight you wish to move, and it will be highlighted in red. Next, click on the destination square, and the knight will move to that square. when you win, an alert window will tell you that you've done it, and how many moves you took. Try and do it in as few moves as possible:
So, what's your record for fewest moves? For that matter, what is the fewest number of moves, and how that we prove that?
At this point, many people would probably throw up their hands in frustration, as analyzing the problem and minimizing the number of moves needed doesn't sound like much fun.
Part of the reason I enjoy mathematical puzzles, and indeed mathematics itself, is the sheer joy of seeing a seemingly complex idea turned into a simple one. This is one of those cases.
Here is the original answer given by Henry Dudeney, along with his original illustrations:
The fewest possible moves, counting every move separately, are sixteen. But the puzzle may be solved in seven plays, as follows, if any number of successive moves by one frog count as a single play. All the moves contained within a bracket are a single play; the numbers refer to the toadstools: (1—5), (3—7, 7—1), (8—4, 4—3, 3—7), (6—2, 2—8, 8—4, 4—3), (5—6, 6—2, 2—8), (1—5, 5—6), (7—1).That's simple and elegant. Take the way in which the knights (or toads) can move, and break them down into a circle. Once you see that, it's quite simple to see AND understand the answer, isn't it?
This is the familiar old puzzle by Guarini, propounded in 1512, and I give it here in order to explain my "buttons and string" method of solving this class of moving-counter problem.
Diagram A shows the old way of presenting Guarini's puzzle, the point being to make the white knights change places with the black ones. In "The Four Frogs" presentation of the idea the possible directions of the moves are indicated by lines, to obviate the necessity of the reader's understanding the nature of the knight's move in chess. But it will at once be seen that the two problems are identical. The central square can, of course, be ignored, since no knight can ever enter it. Now, regard the toadstools as buttons and the connecting lines as strings, as in Diagram B. Then by disentangling these strings we can clearly present the diagram in the form shown in Diagram C, where the relationship between the buttons is precisely the same as in B. Any solution on C will be applicable to B, and to A. Place your white knights on 1 and 3 and your black knights on 6 and 8 in the C diagram, and the simplicity of the solution will be very evident. You have simply to move the knights round the circle in one direction or the other. Play over the moves given above, and you will find that every little difficulty has disappeared.
This simple puzzle has spawned a number of variations. Martin Gardner offered a simple one that deepens the understanding of the method behind this puzzle. In this version, you start the same way, except that one of the white knights is replaced with a red one (so you have two black knights, a white knight, and a red knight). This time, the challenge is two switch the places of the red knight and the white knight in as few moves as possible. Can you do it?
Nope, you can't do it. Why not? All you have to do is go back to the circle (illustration C above). Lay out your starting point in the circle. for example, with the white knight at 1 and the red knight at 3. Whether you go clockwise or counterclockwise, the red knight and white knight will never switch places, as there is no way for knights to jump each other in this puzzle.
Another variation, which Dudeney mentions in the same book as the original version is known as the Penny Puzzle. In this version, there's a board as shown here. You have to set down a penny on any empty circle, and slide it along either straight connecting line to another empty circle. The challenge is to place 7 pennies on the puzzle in this manner, without getting stuck. You can play an online version at this link.
As noted in the Scam School episode just below the puzzle, Chico Marx has even used a version of this with dollar bills to scam people out of money! Both the Penny Star Puzzle version and dollar bill versions work on the same idea as the Knight Shift puzzle above, but require a little different thinking due to the rules about movement.
Once you've got the hang of the previous versions, here's one last challenging version to try. The version at that link uses a 3 by 4 chessboard, and challenges you to switch the positions of 6 knights! Yes, this one can be done, but can you properly analyze it?
The site gives a solution if you get frustrated, but it doesn't give you the why behind the solution. Even if you break down and peek at the solution, try and analyze the solution in a similar manner to the way we did above.
What makes this one so tricky is that it doesn't break down into a nice neat circle, but it does break down into a simpler shape. Martin Gardner shows the breakdown of the 6-knight version here.
If you challenge your friends with this puzzle, I'd love to hear about any interesting experiences you have, or insights you developed. Write about them in the comments!
Posts
No Response to "Knight Shift"
Post a Comment