It's one thing to be able to do math well, whether on paper or in your head. It's often quite another thing to be able to keep the problem in context as you work through it.

Today, Grey Matters features puzzles concerning the ability to keep your numbers in context. The answers will be posted at the end of Thursday's post. Until then, feel free to post your answers in the comments.

• I'll start off with a fairly easy one to get the ball rolling. Watch the Abbott and Costello routine below, where Costello is trying to collect his pay. It starts at $365, and gets whittled down to $1 by Abbott's fast talking. He does it so well that it does make you wonder, what is wrong with Abbott's math? Just for fun, is it possible to work out how much Costello should receive?



• This next puzzle comes from J. Newton Friend's 1954 book Numbers: Fun & Facts, by way of the Futility Closet blog:

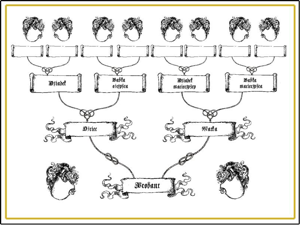
Here is a curious problem. We may safely assume that you had two parents; each of your parents had two parents, so that you had four grandparents. Arguing along similar lines you must have had eight great grandparents and so on. Assuming an average of three generations per century the number of your ancestors since the Christian Era began must have been nearly 1 trillion–

1,000,000,000,000,000,000 or 10¹⁸

This is vastly more people than have ever lived on the Earth. What can we do about it?

Obviously, this can't be right, but where is the flaw?

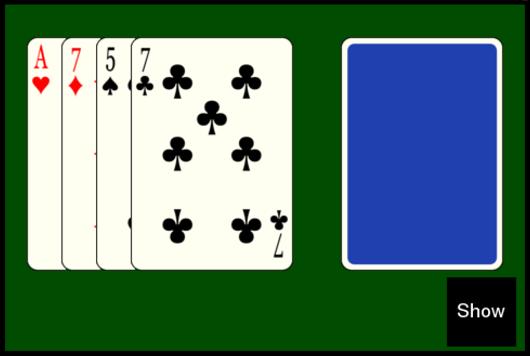
• This next puzzle requires familiarity with the Fitch Cheney 5 Card Trick, as taught in the previous post. A friend of mine was using the app mentioned in that post, and was shown the arrangement you see below. He stated that the face down card was the 7 of Hearts. If you know the trick, this seems to be the right card, but he was incorrect. What is the face-down card?



• Our final puzzle also deals with cards, but in the much more familiar game of Poker. In 5-card Poker, a straight flush (5 cards of consecutive value, all of the same suit) beats 4 of a kind (4 cards of the same value).

How many straight flushes are there? A straight flush can be as low as Ace through 5, or as high as 10 through Ace, so in any given suit, there are 10 possible straight flushes. Multiplying this by the 4 suits gives us 40 possible straight flushes.

How many 4 of a kind hands are there? They can consist of anything from 4 twos up to 4 Aces, so they can be any one of 13 different values. That means there are 13 different 4 of a kind hands.

This brings up an interesting question. If there are 40 ways to get a straight flush, but only 13 ways to get 4 of a kind, that means there are fewer ways to get 4 of a kind than a straight flush. In that case, why does a straight flush beat 4 of a kind?

As I mentioned above, answer the puzzles as best you can in the comments!