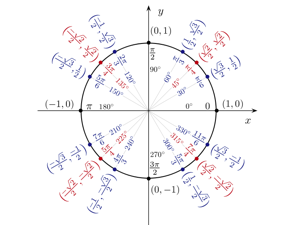
I've posted a new tutorial over at the Mental Gym. It's designed to help you better understand and remember one of the most feared structures in mathematics: The Unit Circle!

Because the unit circle combines pi, degrees, radians, circles, triangles, sines, cosines, and cartesian coordinates, it can often seem intimidating and confusing. I'd tried to break it down clearly and simply, and build it up step-by-step, so that everything was clear.

Naturally, I wanted you to be able to remember it, so there are mnemonics and videos throughout that will help lock all the concepts in your memory. By the time you're done with this tutorial, you'll be calculating sines and cosines of angles with nothing more than your brain and your fingers!

At one point, I even use the Pythagorean theorem to advance understanding of the unit circle. Since the Mental Gym Unit Circle tutorial speaks for itself, I'll spend the rest of this post on the Pythagorean theorem as a sort of bonus.

As you probably remember from high school, if you draw a right (90°) triangle, the side opposite that 90° angle is the hypotenuse, and the other two sides are simply referred to as a and b. The Pythagorean theorem states that, in a right triangle:



Usually, it's simply stated this way:



The more you examine this formula and the effects behind it, the more startling and beautiful its simplicity becomes. It can even be proved without words:


Often, in school, you're given two major types of problems concerning the Pythagorean theorem. In the first type, you're given two sides, such as a side of length 3 and a side of length 4, and asked to find the length of the hypotenuse. In our 3 and 4 example, we would work it out this way:



In the other type, you're given the length of one side and the length of the hypotenuse, and have to work out the length of the remaining side. If we're given 5 as the length of one side, and 13 as the length of the hypotenuse, we work it out like this:



Notice that the answers always seem to magically work out to be whole numbers. Any set of three whole numbers that fits into the Pythagorean theorem is known as a Pythagorean triple. If you click on that link, you'll see that plenty of them are known, and others aren't difficult to find.

Here's a different sort of Pythagorean theorem problem that requires a different sort of approach. It's so different, that you'll probably never encounter it in the average school quiz. Let's say you're given a side length of 8, and asked to find all the possible Pythagorean triples with whole number answers involving 8. Surprisingly, it's easier than you think, with a little help from the following slideshow.