It's Sunday, and that means it's time for the last of Werner Miller's devious magic square puzzles!

I'd like to thank Werner Miller publicly for very generously devising these puzzles, and letting me share them with you. Next Sunday, Grey Matters will return to its regular blog posts, and the answer to this puzzle will appear at the end.

For those who are new, here are the basic rules of the puzzle:

You're given the same set of 4 starting numbers grouped together in similar locations in a 3 by 3, 4 by 4, and 5 by 5 grids. The object is to fill out the grids with other numbers in such a way that the following conditions are satisfied when the grid is completed:

1) Only positive whole numbers are used.

2) No number is duplicated in a single grid (the same number may be used once in each of the 3 grids, however).

3) Each row, each column, and both diagonals of a single grid must total the same sum. All 3 grids in a puzzle, however, are not required to have the same sum (and usually won't). In other words, each grid must be a magic square, but all 3 grids do not have to have the same magic square total.

4) Puzzles will be posted here each Sunday, with the answers to a given puzzle being made available the following Sunday.

3 by 3 grid:


4 by 4 grid:


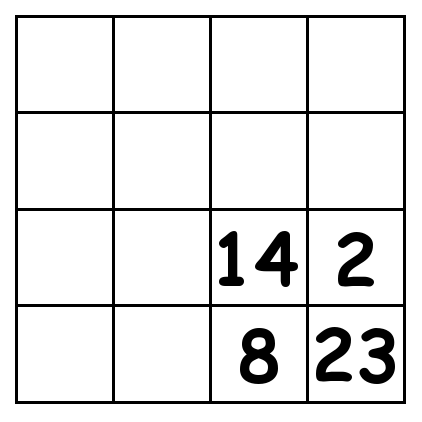
5 by 5 grid:


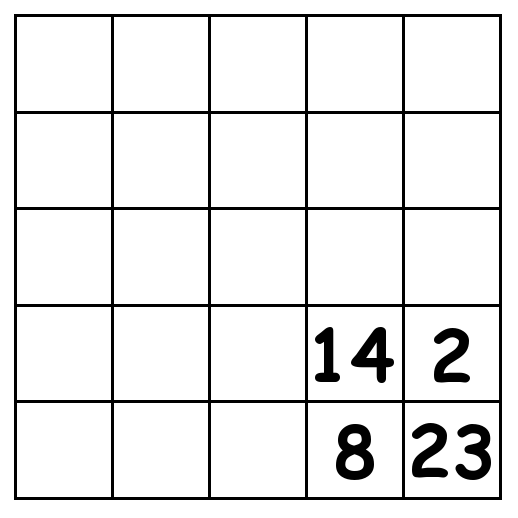
Can you get the answers to these magic square puzzles? If you can solve it before next Sunday, let me know in the comments! You can either describe your solution there, as best as you can, or link to a graphic of your solution.
––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Answers to last Sunday's puzzle:

3 by 3 grid:


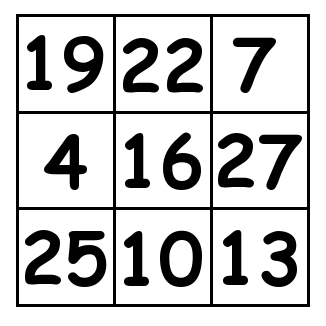
4 by 4 grid:


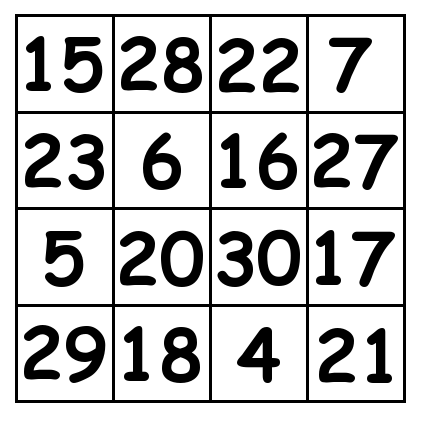
5 by 5 grid: