On August 21, 2017, there will be a total solar eclipse visible in the United States, which hasn't happened since 2012, and won't happen again until 2024!

It's the perfect time to present an impressive knowledge of the moon, such as being able to estimate the moon phase for any date in 2017! Does learning this feat sound difficult? Surprisingly, it's much easier than you may think.

For 2017 only, the phase of the moon formula is simple: (Month key number + date) mod 30. The result is the age of the moon in days from 0 to 29. I'll explain each part of this formula below.

Month key number: January's key number is 3, February's key number is 4, and all other months' keys are their traditional numbers; March is 3, April is 4, May is 5, and so on up to December, which is 12.

Date: This is simply the number represented by the particular date in the month. For the 1st, add 1. For the 2nd, add 2. For the 3rd, add 3, and so on.

mod 30: If you get a total of 30 or more, simply subtract 30. Otherwise, just leave the number as is.

As an example, let's try the published date of this post, July 28th. July is the 7th month and the date is the 28th, so we work out 7 + 28 = 35. Since that number is greater than 30, we subtract 30 to get 35 - 30 = 5. This result tells us that the moon's age will be 5 days on July 28th, 2017.

But what does it mean to say that a moon is some number of days old? Here's a simple explanation:

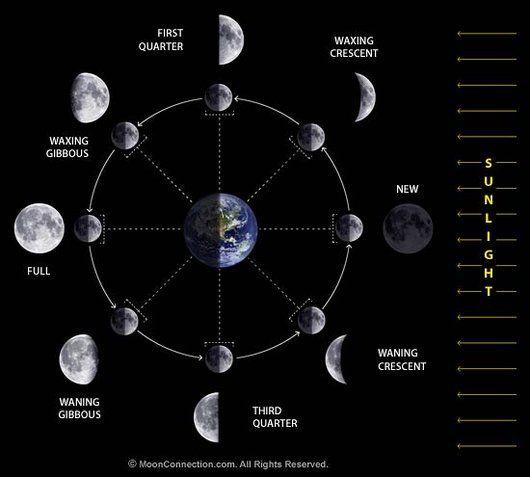
0 days = New moon (the moon is as dark as it's going to get)

0 to 7.5 days = Waxing crescent (Less than half the moon is lit, and it's getting brighter each night)

7.5 days = 1st quarter moon (Half the moon is lit, and getting brighter each night)

7.5 to 15 days = Waxing gibbous (More than half the moon is lit, and getting brighter each night)

15 days = Full moon (The moon is as bright as it's going to get, and will start getting darker each night)

15 to 22.5 days = Waning gibbous (More than half the moon is lit, and it's getting darker each night)

22.5 days = 3rd quarter moon (Half the moon is lit, and it's getting darker each night)

22.5 to 29 days = Waning crescent (Less than half the moon is lit, and it's getting darker each night)

So, our 5-day-old moon would be a waxing crescent (Less than half the moon is lit, and it's getting brighter each night). Sure enough, Wolfram|Alpha confirms this estimate! Moon Giant confirms this estimate, as well.

There are a couple of finer points to note. First, this simple method happens to work only in 2017. The method won't be this simple again until 2036 and then 2055. If you want to learn to calculate the moon phase for any date in the 1900s, you can learn the full feat over in the Grey Matters Mental Gym.

Second, remember that this is an estimate. The actual error margin is plus or minus one day. So, getting an estimate of 5 days means that the moon is somewhere from 4 to 6 days old. When the overlap includes a first quarter moon, a full moon, or a 3rd quarter moon, I usually describe this as, "While it might not be technically accurate, most people would look up and describe it as a 1st quarter moon" (or full moon, or 3rd quarter moon).

This method is a simplification of John Conway's original moon phase estimation formula from Winning Ways for Your Mathematical Plays, vol. 4. Practice it and have some fun amazing your friends and family during the coming solar eclipse!

I recently ran across a number of videos I figured would be interesting to regular Grey Matters readers, so I thought I would share them.

We'll start things off with a little math magic, courtesy of Tom London and his appearance on America's Got Talent earlier this week:



Yes, I could explain the method, but I don't want to ruin the fun and the mystery. Just enjoy the magic of the prediction for what it is, since that's how it's meant to be enjoyed.

If you want mathematical explanations, however, I highly recommend checking out PBS Digital Studios' Infinite Series. These are videos on assorted advanced mathematical topics, yet they're taught in a very accessible way. Back in March, I discussed a puzzle which required the understanding of Markov chains to solve. Compare that to their video Can a Chess Piece Explain Markov Chains?, which also happens to employ my favorite chess piece, the knight:



If you enjoy Grey Matters, you may also the work of 4-time USA memory champion Nelson Dellis, who focuses on both mental and physical fitness. He has a series of memory technique videos, as well as interviews with masters of mental skills. Both of these are available on his YouTube channel, as well. As a taste of his skilll, watch his video, Memorizing 28 names in less than 60 seconds!:



Curious how he's able to do that? He explains in the next video in the series, HOW TO // "Memorizing 28 names in less than 60 seconds!".

At this point, I'll wrap things up so you can get started on a potentially mind-expanding journey.

Ever since I started this blog, I've been waiting for this day. I started Grey Matters on 3/14/05, specifically with the goal of having its 10th blogiversary on the ultimate Pi Day: 3/14/15!

Yes, it's also Einstein's birthday, but since it's a special blogiversary for me, this post will be all about my favorite posts from over the past 10 years. Quick side note: This also happens to be my 1,000th published post on the Grey Matters blog!

Keep in mind that the web is always changing, so if you go back and find a link that no longer works, you might be able to find it by either searching for a new place, or at least copying the link and finding whether it's archived over at The Wayback Machine.

2005

Happy New Year!

With a new calendar year, you deserve a couple of new calendar feats to go with it. In this post, you'll learn how to quickly give the day of the week AND the moon phase for any date in 2015.

Even better, both of these feats are much easier than they sound!

DAY OF THE WEEK FOR ANY DATE IN 2015: The method to do this is quite simple, and is known as the Doomsday method, originally developed by John Horton Conway.

Start by going to last week's post, Calendar Calculation Made Simple, and learning the simple calendar calculation techniques taught there.

To work out dates in only 2015, all you have to remember is that 2015's "Doomsday" is Saturday. If you think about it, you can already work out any date in February using just this knowledge.

For example, Valentine's Day, Feb. 14th, must also be a Saturday, because it's exactly 2 weeks before Feb. 28th. How about Feb. 2nd (Groundhog Day)? Well, Feb. 7th is a Saturday, and Feb. 2nd is 5 days before that. What's 5 days before a Saturday? The answer is Monday! Therefore, Groundhog Day will be on Monday in 2015.

On which day will Christmas fall in 2015? We know from the technique taught in last week's videos that December 12th is a Saturday, so 2 weeks later, December 26th, is also a Saturday. Since Christmas is one day before that, it must be on a Friday!

When is July 4th this year? It's exactly 1 week before July 11th, so it must be a Saturday, as well.

St. Patrick's Day, March 17th, is 3 days after March 14th (Pi Day, mentioned in the videos from last week), so it's 3 days after a Saturday, making it a Tuesday in 2015.

January 15th is Martin Luther King, Jr.'s birthday, but what day does it fall on in 2015? January 3rd is a Saturday this year, and so is January 17th (2 weeks later). Take back 2 days, and we get January 15th being a Thursday this year!

With the knowledge from last week's videos, and a little practice, you can quickly and easily determine the day of the week for any 2015 date. You could get practice at the Day For Any Date (Mentalist Challenge) page, changing the year to 2015, and then trying to determine the date before you click the Show button.

When you're demonstrating this ability for someone, it's nice to be able to prove that you're right about the date. I use Wolfram|Alpha and/or timeanddate.com's calendars.

MOON PHASE FOR ANY DATE IN 2015: 2 years ago, I posted a new tutorial about determining the moon phase for any date. Similar to the year calculations, focusing on a particular year, such as 2015, greatly simplifies the required calculations. Like the doomsday algorithm above, this formula was also developed by John Conway.

In fact, working out the moon phase for any date in 2015 is even simpler than working out the date! How simple is it?

(Month key number + date + 8) mod 30

It's probably best if I explain each part:

Month key number: January's key number is 3, February's key number is 4, and all other months' keys are their traditional numbers; March is 3, April is 4, May is 5, and so on up to December, which is 12.

Date: This is simply the number represented by the particular date in the month. For the 1st, add 1. For the 2nd, add 2. For the 3rd, add 3, and so on.

+ 8: The addition of 8 takes the starting point of 2015 into account, which is why this particular formula works ONLY for 2015.

mod 30: If you get a total of 30 or more, simply subtract 30. Otherwise, just leave the number as is. Betterexplained.com has an intuitive explanation of modular arithmetic.

The resulting number will be the approximate age of the moon in days, from 0 to 29. This formula only gives an approximation, so there's a margin of error of ±1 day.

As an example, let's figure the phase of the moon on July 4, 2015. July is the 7th month, and the 4th is the date, so we work out (7 + 4 + 8) mod 30 = (11 + 8) mod 30 = 19 mod 30, which is just 19.

In that example, we estimate the age of the moon to be 19 days old.

What exactly does the age of the moon in days mean in practical terms? Here's a quick guide:

• 0 days = New moon (the moon is as dark as it's going to get)
• 0 to 7.5 days = Waxing crescent (Less than half th moon is lit, and it's getting brighter each night)
• 7.5 days = 1st quarter moon (Half the moon is lit, and gets brighter each night)
• 7.5 to 15 days = Waxing gibbous (More than half the moon is lit, and getting brighter each night)
• 15 days = Full moon (The moon is as bright as it's going to get, and will start getting darker each night)
• 15 to 22.5 days = Waning gibbous (More than half the moon is lit, and it's getting darker each night)
• 22.5 days = 3rd quarter moon (Half the moon is lit, and gets darker each night)
• 22.5 to 29 days = Waning crescent (Less than half the moon is lit, and it's getting darker each night)

Note: This post first appeared on Grey Matters in 2007. Since then, I've made it a sort of annual tradition to post it every December, with the occasional update. Enjoy!

Since the focus of this blog is largely math and memory feats, it probably won't be a surprise to learn that my favorite Christmas carol is The 12 Days of Christmas. After all, it's got a long list and it's full of numbers!

On the extremely unlikely chance you haven't heard this song too many times already this holiday season, here's John Denver and the Muppets singing The 12 Days of Christmas:



The memory part is usually what creates the most trouble. In the above video, Fozzie has trouble remembering what is given on the 7th day. Even a singing group as mathematically precise as the Klein Four Group has trouble remembering what goes where in their version of The 12 Days of Christmas (Their cover of the Straight No Chaser version):



Just to make sure that you've got them down, I'll give you 5 minutes to correctly name all of the 12 Days of Christmas gifts. Those of you who have been practicing this quiz since I first mentioned it back in 2007 will have an advantage.

Now that we've got the memory part down, I'll turn to the math. What is the total number of gifts are being given in the song? 1+2+3 and so on up to 12 doesn't seem easy to do mentally, but it is if you see the pattern. Note that 1+12=13. So what? So does 2+11, 3+10 and all the numbers up to 6+7. In other words, we have 6 pairs of 13, and 6 times 13 is easy. That gives us 78 gifts total.

As noted in Peter Chou's Twelve Days Christmas Tree page, the gifts can be arranged in a triangular fashion, since each day includes one more gift than the previous day. Besides being aesthetically pleasing, it turns out that a particular type of triangle, Pascal's Triangle, is a great way to study mathematical questions about the 12 days of Christmas.

First, let's get a Pascal's Triangle with 14 rows (opens in new window), so we can look at what it tells us. As we discuss these patterns, I'm going to refer to going down the right diagonal, but since the pattern is symmetrical, the left would work just as well.

Starting with the rightmost diagonal, we see it is all 1's. This represents each day's increase in the number of presents, since each day increases by 1. Moving to the second diagonal from the right, we see the simple sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12, which can naturally represent the number of gifts given on each day of Christmas.

The third diagonal from the right has the rather unusual sequence of 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91. This is a pattern of triangular numbers.

But what can triangular numbers tell us about the 12 days of Christmas? If you look at where the 3 in this diagonal, it's southwest (down and to the left) of the 2 in the second rightmost diagonal. If, on the 2nd day of Christmas, you gave 2 turtle doves and 1 partridge in a pear tree, you would indeed have given 3 gifts, but does the pattern hold? On the 3rd day, you would have given 3+2+1 (3 French hens, 2 turtle doves and a partridge in a pear tree) or 6 gifts total, and sure enough, 6 can be found southwest of the 3! For any of the 12 days, simply find that number, and look to the southwest of that number to see how many gifts you've given by that point! Remember when figured out that the numbers 1 through 12, when added, totaled 78? Look southwest of the 12, and you'll find that same 78!

Let's get really picky and technical about the 12 days of Christmas. It clearly states that on the first day, your true love gave you a partridge in a pear tree, and on the second day your true love gave you two turtle doves and a partridge in a pear tree. You would actually have 4 gifts (counting each partridge and its respective pear tree as one gift) by the second day, the first day's partridge, the second day's partridge and two turtle doves. By the third day, you would have 10 gifts, consisting of 3 partridges, 4 turtle doves and 3 French hens.

At this rate, how many gifts would you have at the end of the 12th day? Sure enough, the pattern of 1, 4, 10 and so on, known as tetrahedral numbers, can be found in our Pascal's Triangle as the 4th diagonal from the right.

If you look at the 2nd rightmost diagonal, you'll see the number 2, and you'll see the number 4 two steps southwest (two steps down and to the left) of it, which tells us you'll have 4 gifts on the second day. Using this same method, you can easily see that you'll have 10 gifts on the 3rd day, 20 gifts on the 4th day, and so on. If you really did get gifts from your true love in this picky and technical way, you would wind up with 364 gifts on the 12th day! In other words, you would get 1 gift for every day in the year, not including Christmas itself (also not including February 29th, if we're talking about leap years)! Below is the mathematical equivalent of this calculation:



If you're having any trouble visualizing any of this so far, Judy Brown's Twelve Days of Christmas and Pascal's Triangle page will be of great help.

One other interesting pattern I'd like to bring up is the one that happens if you darken only the odd-numbered cells in Pascal's Triangle. You get a fractal pattern known as the Sierpinski Sieve. No, this won't tell you too much about the 12 days of Christmas, except maybe the occurrences of the odd days, but it can make a beautiful and original Christmas ornament! If you have kids who ask about it, you can always give them the book The Number Devil, which describes both Pascal's Triangle and Sierpinski Sieve, among other mathematical concepts, in a very kid-friendly way.

There's another 12 Days of Christmas calculation that's far more traditional: How much would the 12 gifts actually cost if you bought them? PNC has been doing their famous Christmas Price Index since 1986, and has announced their results. Rather than repeat it here, check out their site and help them find all 12 gifts, so that you can some holiday fun and then find out the total!

Since my Christmas spending is winding up, I'm going to have to forgo the expensive version, in favor of Miss Cellania's internet-style version of The 12 Days of Christmas. Happy Holidays!

People are often confused as to why the dates of Easter moves around so much from year to year. It moves so much much because Easter is the first Sunday after the first full moon after the first day of spring.

If this sounds confusing on its own, consider that the Roman Catholic and Eastern Orthodox churches use different calendars, which can yield different dates as a result!

Thanks to the work of John Conway, though, it is possible to work out the date of both Roman Catholic and Orthodox Easters in your head!

Some basic understanding and practice are all that's really needed to be able to calculate the Easter date in your head for any year from 1900 to 2099. In order to help make everything clearer, I've posted my new Easter Date For A Given Year tutorial over in the Mental Gym. To make it easier to learn, the tutorial is broken up into several steps:

• The introduction explains the rules for Easter calculation in detail, as well as what you need to know to get started.

• The next section explains how to calculate the date of the traditional Roman Catholic Easter. After learning how to work out the date of the Paschal full moon (the first full moon after the first day of spring in a given year), you then learn how to work out the date of Easter for that same year.

• If you want to impress others by performing this feat, there's an entire section of presentation tips that can help make this feat entertaining.

• The method for calculating the date of Orthodox Easter is covered another section, as well. Assuming you can work out Roman Catholic Easter, there are surprisingly few changes involved in working out the Orthodox Easter date.

• Finally, there's another section for those adventuresome souls who want to venture on and work out Easter dates in other centuries. Here you can find out what changes need to be made to the original calculations.

Since practice is important, I've also developed a set of interactive Easter date quizzes. Since you work through each section verbally in a step-by-step manner, the quizzes work the same way. In the first quiz, you simply work out the paschal full moon date for Roman Catholic Easter. In the next quiz, you're asked about the paschal full moon and Easter dates. The Orthodox quizzes are similar, and start with the Roman Catholic dates first, since you need that information as a starting point.

If you put in a little understanding, a little practice, and a little time, you may surprise yourself (and others) with an impressive new skill!

June's snippets are ready!

This month, we're going back to some favorite topics, and provide some updates and new approaches.

• Let's start the snippets with our old friend Nim. The Puzzles.com site features a few Nim-based challenges. The Classic Nim challenge shouldn't pose any difficulty for regular Grey Matters readers.

Square Nim is a bit different. At first glance, it might seem to be identical to Chocolate Nim, but there are important differences to which you need to pay attention.

Circle Nim is a bit of a double challenge. First, you may need to try and figure it out. Second, the solution is images-only. Once you realize that different pairs of images are referring to games involving odd or even number starting points, it shouldn't be too hard to understand.

• Check out the Vanishing Leprechaun trick in the following video:



These are what are known as geometric vanishes, and can be explored further in places such as Archimedes' Laboratory and the Games column in the June 1989 issue of OMNI Magazine.

Mathematician Donald Knuth put his own spin on these by using the format to compose a poem called Disappearances. If you'd like to see just how challenging it is to compose a poem in geometric vanish form, you can try making your own in Mariano Tomatis' Magic Poems Editor.

• Back in July 2011, I wrote a post about hyperthymesia, a condition in which details about every day of one's life are remembered vividly. That post included a 60 Minutes report about several people with hyperthymesia, including Taxi star Marilu Henner. Earlier this year, 60 Minutes returned to the topic with a new story dubbed Memory Wizards. This updated report is definitely worth a look!

• If you're comfortable squaring 2-digit numbers, as taught in the Mental Gym, and you think you're ready to move on to squaring 3-digit numbers, try this startlingly simple technique from Mind Math:



That's all for June's snippets. I hope you have fun exploring them!

It's been over a year since I posted a tutorial over at the Mental Gym, so I figured it was about time for a new one!

This one is a new spin on working out the calendar for a given month and year. Yes, I have an existing Day of the Week For Any Date tutorial, and even a commercially-available version, but this new one is remarkably simple!

The new tutorial is dubbed the Quick Calendar Month Creation. It's a combination of a little-known, yet surprisingly simple calendar calculation method published by W. W. Durbin and E. Rogent in 1927, Robert Goddard's First Sunday Doomsday Algorithm, and my own approach of creating a full-month calendar to was calculations.

For those familiar with Doomsday algorithm, this isn't yet another variation of John Conway's fine work. Instead, I started with Durbin and Rogent's unusual and simple approach to dealing with the year, and adjusted the math so it meshed with Goddard's powerful work. The exact details and credits are given at the bottom of each section of the tutorial.

The result is a calendar creation routine that's quick and simple to learn, yet powerful enough to let you create calendar for any month and year back to 45 B.C., when the Julian calendar was first used!

To help you practice it more effectively, I've also developed a quiz page. The initial quizzes are simple, in order to help you master the calculation and recall required by each step, and then there's a more complete quiz, which simply has you create a calendar month for random dates. Some of you may recognize this as a modified version of my calendar quiz from Day One.

If you've never tried to do a calendar calculation before, try this out, and you might surprise yourself. If you've tried to do calendar calculations before and given up because of the difficulty of other methods, try the Quick Calendar Month Creation tutorial, and see the ease and power of this approach. Either way, I'd love to hear what you think about it in the comments!

It's time to train and strain your brain to entertain!

This time around, we're going to take another look at finding 5th roots. Imagine having someone choose a secret number x, multiplying it by itself a total of 5 times, as in x × x × x × x × x, giving you only the answer, and you're able to work out what the original number x!

It was almost a year ago when Scam School covered how to do cube roots in your head. If you practiced that, you may still be worried about handling 5th roots.

Surprisingly, doing 5th roots in your head is actually easier! Numberphile, with some help from Simon Pampena, explains the process in the following video:



Want to practice this feat for yourself? I have a detailed tutorial on working out 5th roots in your head along with a 5th root quiz designed to help you master this feat. Michael Daniel's Mind Magician site also features a different, but still excellent, 5th root tutorial and quiz, too.

There's little you can do with this other than using it to impress people at parties, but with 5th roots, cube roots, and perhaps even square roots of perfect squares and square roots of non-perfect squares, you'll have plenty of tools in your bag to astound and amuse when the time is right!

For January's snippets, I'm featuring an unusual mix.

This time around, I've got 3 different things for you: Math, memory...and Macs?!?

• Numberphile took a breather from their usual number videos to do something a bit different. They interviewed UC Berkeley professor Edward Frenkel with the question, “Why do people hate mathematics?” It's an interesting topic and well worth your time:



• In the video above, they talk about the important roles of math teachers. Longtime Grey Matters readers know that I'm not just a big proponent of memorizing, but rather memorizing along with understanding. Above and beyond great sites that aid in mathematical understanding, such as BetterExplained and Plus magazine, there's also an excellent free ebook called Nix The Trix. It's aimed at students who are great with shortcuts, but never took the time to understand the foundations of what those tricks are actually doing. It can help teachers undo the damage by showing how to teach the actual mathematical basis, which is also a great help in understanding when to use the math tricks.

• Almost just in time for this month's snippets, Reddit featured an interesting and popular thread asking, “What are some things worth memorizing?” Yes, of course, there are the usual array of sarcastic and silly answers, but if you take the time to wade through some of the roughly 12,000 comments (at this writing), there are some great ideas. I won't rob you of the joy of discovery, especially as the reply you most enjoy may not even exist yet as I write this!

• If you've ever memorized something with the help of spaced learning, where the concept you're trying to memorize is reinforced 3 times at spaced intervals, you know how powerful it can be. There's now an online web service called MemStash which help you do this almost automatically. You save things you wish to remember by highlighting them in an online page, and then clicking a special MemStash bookmarklet. After that, they'll send you 3 reminders at spaced intervals, which can help you recall what you saved!

• OK, this last snippet isn't really along the usual Grey Matters topics, but I thought it would be fun to sneak it in. 30 years ago this week, the Apple Macintosh computer first came on the market. During Super Bowl XVIII on January 22, 1984, they aired their now-classic 1984 ad, announcing the upcoming release of the Macintosh on January 24th. The lesser-known January 24, 1984 introduction of the Macintosh has also been preserved on video:



That's all for this month's snippets. I hope you enjoy them!

No, I'm not just putting random filler text in the title.

Ever hear the expression “the oldest trick in the book”? In this post, you'll learn about a card trick that certainly qualifies, as it's known to date back at least as far as 1769!

I'll start by letting Brian Brushwood perform and explain his version of this classic routine (YouTube link):



Now, you'll note that Brian teaches this with the words:

MUTUS
NOMEN
DETID
COCIS

BIBLE
ATLAS
GOOSE
THIGH

LIVELY
RHYTHM
MUFFIN
SUPPER
SAVANT

PILLAR
RHYTHM
MUFFIN
CACTUS
SNOOPY

MEACOCK
RODDING
GUFFAWS
TWIZZLE
RHYTHMS
KNUBBLY

Happy New Year!

With a new calendar year, you deserve a couple of new calendar feats to go with it. In this post, you'll learn how to quickly give the day of the week AND the moon phase for any date in 2014.

Even better, both of these feats are much easier than they sound!

DAY OF THE WEEK FOR ANY DATE IN 2014: The method to do this is quite simple, and is known as the Doomsday method, originally developed by John Horton Conway. Don't worry, learning this method for one particular year is very simple.

The "Doomsday" from which the method gets its name always refers to the last day of February, whether it's the 28th or 29th. For 2014, the "Doomsday" is Friday (Feb. 28th, since it's not a leap year). If you think about it, you can already work out any date in February using just this knowledge.

For example, Valentine's Day, Feb. 14th, must also be a Friday, because it's exactly 2 weeks before Feb. 28th. How about Feb. 2nd (Groundhog Day)? Well, Feb. 7th is a Friday, and Feb. 2nd is 5 days before that. What's 5 days before a Friday? The answer is Sunday! Therefore, Groundhog Day will be on Sunday in 2014.

It's also fairly simple to learn the even-numbered months. There's a very simple pattern to remember them: 4/4 (April 4th), 6/6 (June 6th), 8/8 (August 8th), 10/10 (October 10th), and 12/12 (December 12th) will always fall on the same day of the week as the "Doomsday" (the last day of February, remember?).

On which day will Christmas fall in 2014? We know December 12th is a Friday, so 2 weeks later, December 26th, is also a Friday. Since Christmas is one day before that, it must be on a Thursday this year!

The odd months aren't much harder, but the patter is not the same. 5/9 (May 9th) and 9/5 (September 5th) will also always fall on the Doomsday, as will 7/11 (July 11th) and 11/7 (November 7th). This is easy to remember with the following simple mnemonic: "I'm working 9 to 5 at the 7-11". It helps you remember that 9 and 5 always go together, as do 7 and 11.

When is July 4th this year? It's exactly 1 week before July 11th, so it must be a Friday, as well. If you've got all the previous dates down, you've already got the mental capability to determine the date for 10 out of the 12 months!

The easiest way to handle March is to think of Feb. 28th as also being "March 0th". Working forward from March 0th, it's easy to see that March 7th, 14th, 21st and 28th will all be Fridays. St. Patrick's Day, March 17th, is 3 days after March 14th, so it's 3 days after a Friday, making it a Monday in 2014.

In January, it's usually the 3rd day of the month that falls on the Doomsday. In a leap year, however, January 4th falls on the Doomsday. Remember it this way: "3 times out of 4, it's January 3rd. On the 4th year, it's January 4th." In 2014, since it's not a leap year, you only have to recall that January 3rd is on the Doomsday (Friday, for 2014).

January 15th is Martin Luther King, Jr.'s birthday, but what day does it fall on in 2014? January 3rd is a Friday this year, and so is January 17th (2 weeks later). Take back 2 days, and we get January 15th being a Wednesday this year!

With the above knowledge, and a little practice, you can quickly and easily determine the day of the week for any 2014 date. You could get practice at the Day For Any Date (Mentalist Challenge) page, changing the year to 2014, and then trying to determine the date before you click the Show button.

When you're demonstrating this ability for someone, it's nice to be able to prove that you're right about the date. I use QuickCal on my iPod Touch (similar calendar are available for many portable devices).

MOON PHASE FOR ANY DATE IN 2014: 1 year ago, I posted a new tutorial about determining the moon phase for any date. Similar to the year calculations, focusing on a particular year like 2014 greatly simplifies the required calculations. Like the doomsday algorithm above, this formula was also developed by John Conway.

In fact, working out the moon phase for any date in 2014 is even simpler than working out the date! How simple is it?

(Month key number + date - 3) mod 30

It's probably best if I explain each part:

Month key number: January's key number is 3, February's key number is 4, and all other months' keys are their traditional numbers; March is 3, April is 4, May is 5, and so on up to December, which is 12.

Date: This is simply the number represented by the particular date in the month. For the 1st, add 1. For the 2nd, add 2. For the 3rd, add 3, and so on.

- 3: The subtracting of 3 takes the starting point of 2014 into account, which is why this particular formula works ONLY for 2014.

mod 30: If you get a total of 30 or more, simply subtract 30. Otherwise, just leave the number as is. Betterexplained.com has an intuitive explanation of modular arithmetic.

The resulting number will be the approximate age of the moon in days, from 0 to 29. This formula only gives an approximation, so there's a margin of error of ±1 day.

As an example, let's figure the phase of the moon on July 4, 2014. July is the 7th month, and the 4th is the date, so we work out (7 + 4 - 3) mod 30 = (11 - 3) mod 30 = 8 mod 30, which is just 8.

In that example, we estimate the age of the moon to be 8 days old.

What exactly does the age of the moon in days mean in practical terms? Here's a quick guide:

• 0 days = New moon (the moon is as dark as it's going to get)
• 0 to 7.5 days = Waxing crescent (Less than half th moon is lit, and it's getting brighter each night)
• 7.5 days = 1st quarter moon (Half the moon is lit, and gets brighter each night)
• 7.5 to 15 days = Waxing gibbous (More than half the moon is lit, and getting brighter each night)
• 15 days = Full moon (The moon is as bright as it's going to get, and will start getting darker each night)
• 15 to 22.5 days = Waning gibbous (More than half the moon is lit, and it's getting darker each night)
• 22.5 days = 3rd quarter moon (Half the moon is lit, and gets darker each night)
• 22.5 to 29 days = Waning crescent (Less than half the moon is lit, and it's getting darker each night)

Note: This post first appeared on Grey Matters in 2007. Since then, I've made it a sort of annual tradition to post it every December, with the occasional update. Enjoy!

Since the focus of this blog is largely math and memory feats, it probably won't be a surprise to learn that my favorite Christmas carol is The 12 Days of Christmas. After all, it's got a long list and it's full of numbers!

On the extremely unlikely chance you haven't heard this song too many times already this holiday season, here's John Denver and the Muppets singing The 12 Days of Christmas:



The memory part is usually what creates the most trouble. In the above video, Fozzie has trouble remembering what is given on the 7th day. Even a singing group as mathematically precise as the Klein Four Group has trouble remembering what goes where in their version of The 12 Days of Christmas (Their cover of the Straight No Chaser version):



Just to make sure that you've got them down, I'll give you 5 minutes to correctly name all of the 12 Days of Christmas gifts. Those of you who have been practicing this quiz since I first mentioned it back in 2007 will have an advantage.

Now that we've got the memory part down, I'll turn to the math. What is the total number of gifts are being given in the song? 1+2+3 and so on up to 12 doesn't seem easy to do mentally, but it is if you see the pattern. Note that 1+12=13. So what? So does 2+11, 3+10 and all the numbers up to 6+7. In other words, we have 6 pairs of 13, and 6 times 13 is easy. That gives us 78 gifts total.

As noted in Peter Chou's Twelve Days Christmas Tree page, the gifts can be arranged in a triangular fashion, since each day includes one more gift than the previous day. Besides being aesthetically pleasing, it turns out that a particular type of triangle, Pascal's Triangle, is a great way to study mathematical questions about the 12 days of Christmas.

First, let's get a Pascal's Triangle with 14 rows (opens in new window), so we can look at what it tells us. As we discuss these patterns, I'm going to refer to going down the right diagonal, but since the pattern is symmetrical, the left would work just as well.

Starting with the rightmost diagonal, we see it is all 1's. This represents each day's increase in the number of presents, since each day increases by 1. Moving to the second diagonal from the right, we see the simple sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12, which can naturally represent the number of gifts given on each day of Christmas.

The third diagonal from the right has the rather unusual sequence of 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91. This is a pattern of triangular numbers.

But what can triangular numbers tell us about the 12 days of Christmas? If you look at where the 3 in this diagonal, it's southwest (down and to the left) of the 2 in the second rightmost diagonal. If, on the 2nd day of Christmas, you gave 2 turtle doves and 1 partridge in a pear tree, you would indeed have given 3 gifts, but does the pattern hold? On the 3rd day, you would have given 3+2+1 (3 French hens, 2 turtle doves and a partridge in a pear tree) or 6 gifts total, and sure enough, 6 can be found southwest of the 3! For any of the 12 days, simply find that number, and look to the southwest of that number to see how many gifts you've given by that point! Remember when figured out that the numbers 1 through 12, when added, totaled 78? Look southwest of the 12, and you'll find that same 78!

Let's get really picky and technical about the 12 days of Christmas. It clearly states that on the first day, your true love gave you a partridge in a pear tree, and on the second day your true love gave you two turtle doves and a partridge in a pear tree. You would actually have 4 gifts (counting each partridge and its respective pear tree as one gift) by the second day, the first day's partridge, the second day's partridge and two turtle doves. By the third day, you would have 10 gifts, consisting of 3 partridges, 4 turtle doves and 3 French hens.

At this rate, how many gifts would you have at the end of the 12th day? Sure enough, the pattern of 1, 4, 10 and so on, known as tetrahedral numbers, can be found in our Pascal's Triangle as the 4th diagonal from the right.

If you look at the 2nd rightmost diagonal, you'll see the number 2, and you'll see the number 4 two steps southwest (two steps down and to the left) of it, which tells us you'll have 4 gifts on the second day. Using this same method, you can easily see that you'll have 10 gifts on the 3rd day, 20 gifts on the 4th day, and so on. If you really did get gifts from your true love in this picky and technical way, you would wind up with 364 gifts on the 12th day! In other words, you would get 1 gift for every day in the year, not including Christmas itself (also not including February 29th, if we're talking about leap years)!

If you're having any trouble visualizing any of this so far, Judy Brown's Twelve Days of Christmas and Pascal's Triangle page will be of great help.

One other interesting pattern I'd like to bring up is the one that happens if you darken only the odd-numbered cells in Pascal's Triangle. You get a fractal pattern known as the Sierpinski Sieve. No, this won't tell you too much about the 12 days of Christmas, except maybe the occurrences of the odd days, but it can make a beautiful and original Christmas ornament! If you have kids who ask about it, you can always give them the book The Number Devil, which describes both Pascal's Triangle and Sierpinski Sieve, among other mathematical concepts, in a very kid-friendly way.

There's another 12 Days of Christmas calculation that's far more traditional: How much would the 12 gifts actually cost if you bought them? PNC has been doing their famous Christmas Price Index since 1986, and has announced their results. Rather than repeat it here, check out their site and help them find all 12 gifts, so that you can some holiday fun and then find out the total!

Since my Christmas spending is winding up, I'm going to have to forgo the expensive version, in favor of Miss Cellania's internet-style version of The 12 Days of Christmas. Happy Holidays!

Many in the US are enjoying a lazy 4-day weekend as I write this. That being the case, I'll keep the feats relatively simple.

In this post, you'll find out how to easily give others a new perspective by looking at time and space in new ways!

EARTH PHASE FROM THE MOON: If you've practiced working out the moon phase for any date in your head, whether you do the full version, or just memorized how to do it for 1 particular year, this feat is surprisingly simple.

Once you've determined the phase of the moon on a given date, the phase of the Earth as seen from the moon will be exactly the opposite phase! If the moon, as seen from the Earth, is in a full moon, then the Earth, as viewed from the moon, will be a “New Earth” (the Earth will be unlit). If the moon is in a waxing gibbous phase (more than 50% lit, and getting brighter each night), then the Earth, as seen from the moon, will be in a waning crescent phase (the Earth will be less than 50% lit, and getting darker each night).

Why does it work out this way? Take a look at the moon phase diagram below. Pick a phase, and follow that phase's line from the Earth to the moon, and imagine extending it through the moon. Imagine yourself out in space, along that line, looking at the opposite side of the moon that everyone on Earth sees. It's not hard to understand that the moon on this side must be in the opposite phase. If one side is getting brighter, the other side must be getting darker, and vice-versa.

Now, imagine yourself on that same line, but now you're between the Earth and the moon, facing the Earth. The sun is far enough away (90+ million miles!) that it's going to be lighting the opposite side of the moon and the Earth in the same way.



Just as in the original feat, you can verify this with Wolfram Alpha. If someone asks for the moon phase for, say, December 10, 2014, you would use the standard feat to estimate that the moon would be 19 days old (18-20 days old, including the margin of error), so you'd know it's in a waning gibbous phase, which means the moon is more than 50% lit, and getting darker each night.

Conversely, the Earth, as viewed from the moon, must be in a waxing crescent phase, so the Earth is less than 50% lit, and getting brighter each night. Wolfram Alpha can verify this for you.

1 MILLION SECONDS AGO: When you hear large numbers tossed around, it's really hard to get a sense of scale. How big is something like 1 million? To put it into perspective, imagine we're talking about 1 million seconds. When was it 1 million seconds ago?

Determining this isn't hard, especially if you just want to give the correct date. 1 million seconds is roughly 11.5 days. You can work out in your head what day 12 days ago was, or just cheat and use Wolfram Alpha to find out. If your local time is 1:46 PM or before, 1 million seconds ago was 12 days ago. If your local time is 1:47 PM or after, 1 million seconds ago was 11 days ago.

I'm writing this paragraph on December 1st, 2013, at about 11:45 AM local time, so 1 million seconds ago was November 19th, 2013. If I'm asked this afternoon at, say, 3:30 PM when 1 million seconds ago was, I'd say it was November 20, 2013, instead, because that is after 1:47 PM.

If you're interested in giving the exact minute, take the current time, add 13 minutes, then add 10 hours. 1 million seconds before December 1st at 11:45 AM would be November 19th of the same year at 9:58 PM, because 11:45 AM plus 13 minutes is 11:58 AM, and 10 hours after that is 9:58 PM.

If you're challenged to work out the exact second it was 1 million seconds ago, add 13 minutes and 20 seconds before adding the 10 hours. On 1:46:40 PM local time on any given day, 1 million seconds ago was exactly midnight, heading into 11 days ago.

As always, people can verify your answer using Wolfram Alpha.

1 BILLION SECONDS AGO: Since we're talking about large numbers, many people don't realize the difference in scale between 1 million and 1 billion, so when was 1 billion seconds ago?

1 billion seconds is over 31 years ago, so don't try and work out the exact date in your head. For this one, just look it up in Wolfram Alpha. As I write this on December 1, 2013, 1 billion seconds ago was March 25, 1982.

Working out the exact time is even simpler for 1 billion seconds ago, as it happens. First, add 13 minutes (and 20 seconds, if desired), just as before, but subtract 2 hours instead of adding 10 hours. December 1, 2013 at 11:45 AM minus 1 billion seconds is March 25, 1982 at 9:58 AM. Yes, your calculations can be verified with Wolfram Alpha.

You can make older dates like this more vivid by looking up those days on Wolfram Alpha or Wikipedia's year pages. For example, just a quick scan of those pages, I can remember that Danica Patrick was born, the first computer virus was only 2 months old, and the Vietnam Veteran's Memorial in Washington, D.C. would be opened the next day for the very first time.

1 TRILLION SECONDS AGO: 1 trillion seconds ago is the easiest, because that was 31,689 years ago, before modern clocks or calendars existed. This is roughly around 30,000 BCE, so ideas like the bow and arrow were still new, and not a single person was living in Japan yet. Obviously, if you include this, it's more for the sense of scale as compared to 1 million and 1 billion seconds ago.

If you like more mind-blowing changes in perspective, check out my Astronomical Scale post, and be ready for even more surprises!

Last month's snippets focused on the simple and straightforward side of math.

I thought it might be fun to dabble in the other end of the spectrum, so this month's snippets focus on taming the seemingly complex side of math.

• One interesting mental challenge is what are known as Fermi estimates. These are estimates which are seemingly done with little or no information, yet give an accurate estimate to the nearest power of 10. The folks at TED-Ed produced the following video which explains the concept in more detail:



Learning how to do this can be a little tricky, as you really have to learn as you go. One of the best online tutorials I've run across as of this writing is this FermiQuestions.com tutorial. The more you learn, the better equipped you'll be to answer the sample questions they give at their website.

There's also a great book titled How Many Licks? that focuses on teaching you how to develop your Fermi estimation skills clearly and simply.

• If you enjoyed Vi Hart's video on dragons from August, you'll be glad to know she's produced two more videos in the same series. The second one in the series is called “Dragon Dungeons”:



...and the third in the series is called “Dragon Scales”:



• Speaking of dragons and other mathematical monsters, the Data Genetics blog has just posted an interesting tutorial on how to escape a monster (using calculus). Ideally, you'll have a basic understanding of calculus to understand what is going on in this fun article. Even if you don't, the article is still readable, and you get a good understanding of how the real world relates to the needed calculus.

One of the most feared things students come across is the periodic table of the elements.

They see the sheer number of elements, and all the details such as atomic numbers, weights, and symbols, and it's easy to see why it's considered to be overwhelming. In this post, you can learn to not only tame this beast, but have a little fun with it, as well!

Among the best ways to remember things are by memorizing them in groups, and with a story. YouTube user freegyan gyanlee, with the help of an illustrator friend, is putting out a series of free videos using these techniques to teach the element name, based on the book Memorize the Periodic Table.

Start by learning elements 1 through 10, and when you're comfortable with that story, then move on to the next 10 or so elements. Here is the first video in the series:



The nice thing about the story approach is that, should you desire to remember more about each element, you can attach sillier and more unusual details to the appropriate image. For example, if you wish to remember that boron is the 5th element, you might have the bee being bribed with a $5 bill to bore on the balloon, or perhaps the bee bores on the balloon by accident because he's watching the movie The Fifth Element.

In fact, if you added images to represent just the multiples of 5 to each element (5 to the 5th element, 10 to the 10th, 15 to 15th, and so on), you could make it easy to get the elemental number of almost any element by starting from the named element, and working backwards or forwards to the nearest element with an image for the multiple of 5. For example, what number is nitrogen? Well, we know the night-row general lost his car to a car bomb that resulted when the bee bore on the balloon while watching The Fifth Element, so nitrogen must be 2 elements after number 5, therefore, nitrogen must be element number 7!

At this writing, there aren't video to cover all 118 elements yet. However, there are more than enough to keep you busy:

• Elements 11-20

• Elements 21-30

• Elements 31-40

• Elements 41-50

• Elements 51-63

If you'd like to find out more mnemonics for the periodic table of the elements, check out the Mnemonics Devices for the elements here. As many a memorizer has learned, taking things slow, and making them fun, silly, and unusual is one of the best way to keep things in your mind.

My previous post focused on politics, and this one will focus on the Middle East.

I swear I'm not turning this into a blog about political topics.

Instead of issues in the Middle East, this post will focus on memorizing the names and locations of all the Middle Eastern countries.

Back in January, I posted a series of videos about memorizing regions of the world, produced by YouTube user eveRide. Those videos covered Central America, South America, and Europe.

This past week, he uploaded a brand new video, focusing on the Middle East. Even though India isn't traditionally considered to be in the Middle East, it does serve as a good starting reference point from which to work.



The countries are unlabeled, and their borders can be hard to see in the above video, so below is a reference map that may be of help. Click the map to see a larger version.



From the videos, I gather the producer is a teacher, and tends to make these videos in the fall, presumably for the students. Personally, I enjoy these videos and the creativity used in developing these mnemonics. I'll definitely be keeping an eye on eveRide's channel, and bring you more as they become available.

While going through Mental Floss' Be More Interesting columns mentioned in my previous post, their post on how to navigate with stars caught my attention.

I've posted on how to calculate the moon phase for any date in your head, so why not learn more about the rest of the night sky?

The advice in Mental Floss' star navigation post is good as far as it goes. Yes, there are really only a few constellations you need to know to find your way around the sky, but the column stops short of practical teaching.

A website called quietbay.net used to feature a great tutorial on finding the important constellations, but that site has vanished from the internet. Fortunately, the Internet Wayback Machine has come to the rescue!

Here is the archived version of quietbay's clear, visual, and interactive constellation tutorial. It only takes about 15-20 minutes for the full tutorial. Being an archived version, there are a few images missing here and there, and only once or twice are those missing images are essential to finding the stars in the tutorial, but overall, it's still quite workable, and will quickly teach you how to located Polaris, Betelgeuse, Orion, the Big Dipper, Cassiopeia, and even Jupiter, if it's in the sky.

You should also note that it's a northern hemisphere-based tutorial, so the constellation Crux isn't included. Unless you're viewing from the southern hemisphere or the northern tropics, you won't be able to see Crux. If you can see it, Crux is one of the easier constellations to locate.

Try out the tutorial, read the Wikipedia article on Crux, and practice with the real night sky, and you'll be amazed how quickly you can get a good, basic knowledge of the night sky!

UPDATE: This site goes as far back as 2003. This approach was turned into a book in 2010, titled Stikky Night Skies. It teaches 6 constellations, 4 stars, a planet, and a galaxy, and only takes about an hour to read. There is a sample tutorial on the book's website, teaching only about Orion and Betelguese.

If you'd like to learn more in this same way, I highly recommend Laurence Holt's Stikky Night Skies!

No, I didn't misspell algorithms in the title.

Logarithms are percieved to be very difficult, or even mysterious. If you take the time to understand them, however, they're not mysterious or difficult, and they can even make some things easier for you! Let's get right to the basics.

If you're familiar with exponents, such as 10², logarithms are basically just a way of rearranging the exponent problem in a different way. This video will explain that idea in a little more detail:



While that boils down what logarithms are, the only real use they describe in that video is the pH of pool water, and it doesn't delve into that much. Over at BetterExplained.com, they have a great article on Using Logarithms In The Real World that gives you a better grasp of their importance. It's a must read on the topic!

As you can see in the graphic up in the corner, logs are easily calculated on many calculators, and computers. However, Numberphile has an excellent lesson in working with logarithms without aid from electronics:



Besides showing the use of log tables, this video also introduces one of my favorite aspects of logarithms. It takes most arithmetic operations and simplifies them in an interesting way. Multiplication becomes addition, division becomes subtraction, exponents become multiplication, and roots become division. In short, logarithms can almost seem like cheating, as they turn more difficult operations into simpler ones!

Even though you see seemingly endless pages of log tables in the video above, it is possible to work out logs in your head, and with much less memorization than you might think. I be derelict in my duty at Grey Matters if I didn't show you how to do something along these lines!

Nerd Paradise has an excellent lesson on working out base 10 logs in your head, and the comments feature several great additional tips. CuriousMath.com used to have a similarly great lesson, which has been rescued by the Internet Wayback Machine. The comments here are also quite helpful.

A lesson in working on exponential problems through logs has also been rescued. The 3rd example, involving finding 5th roots, is surprisingly simple, once you've mastered the basics.

You don't even need to do any mental calculation to take advantage of the power of logarithms. Go back and read my Benford's Law post. It features a quick lesson from James Grime and a Scam School video that shows you how to take advantage of Benford's Law in a very clever way.

Take some time and learn about logarithms. There's plenty to discover, learn, and enjoy about them!

August's snippets are here!

This month, our snippets return to their original roots, and are just a mixed bag of goodies I thought might be of interest to Grey Matters readers.

• While reading Numericana, I learned about a trick dubbed Enigma. The video for the performance is shown below:



The explanation video can be found here. However, Grey Matters readers can use their knowledge of quick binary conversion to speed up the needed calculations!

• Speaking of base conversions, here's an unusual fact. For any integers x and y, x^y in base x will always be 1 followed by y zeros! For example, 6⁸ in base 6 is 1 followed by 8 zeros. Here are the number 2 through 6 raised to the second through the tenth power in Wolfram|Alpha, as an example.

• Futility Closet features a simple way to calculate the probability of any number from 2 to 12, when rolling 2 six-sided dice.

• While playing around with memorizing the speed of light in meters per second (299,792,458 m/s), I was originally using the method of using words of a given length to represent a given number (3-letter word to represent 3, etc.). I noticed that it was taking longer to count the longer words, and thought it might be better to combine that technique with words that rhyme.

In other words, use 9-letter words that rhyme with the word NINE, 8-letter words that rhyme with the word EIGHT, and so on. Using sites like WordHippo and RhymeZone, here's what I came up with for the speed of light: “To recombine, valentine, shorten storyline. Do more alive, soulmate!”

That's all for this month's snippets. I hope you enjoyed them!