This week, Diamond Jim Tyler demonstrates a new take on an old trick. Regular Grey Matters readers won't be surprised to learn that I like it because it's based on math, and it's very counterintuitive. We'll start with the new video, and then take a closer look at the trick.

This week's Scam School episode is called The Collective Coin Coincidence, and features Diamond Jim Tyler giving not only a good performance, but also a good lesson in improving a routine properly:



Brian mentions that this was an update from a previous Scam School episode. What he doesn't mention is that you have to travel all the way back to 2009 to find it! The original version was called The Coin Trick That Fooled Einstein, and Brian performed it for U.S. Ski Team Olympic gold medalist Jonny Moseley. It's worth taking a look to see how the new version compares with the original.

Brian and Jim kind of rush through the math shortly after the 4:00 mark, but let's take a close look at the math step-by-step:

Start - The other person has an unknown amount of coins. As with any unknown in algebra, we'll assign a variable to it. To represent coins, change or cents, we'll use: c

1 - When you're saying you have as many coins (or cents) as they do, you're saying you have: c

2 - When you're saying you have 3 more coins than they do, the algebraic way to say that is: c + 3

3 - When you're saying you have enough left over to make their number of coins (c) equal 36, that amount is represented by 36 - c, so the total becomes: c + 3 + 36 - c

Take a close look at that final formula. The first c and the last c cancel out, leaving us with 3 + 36 which is 39. If you go through these same steps with the amount of coins (in cents, as it will make everything easier) as opposed to the number of coins, it works out the same way. This is what Diamond Jim Tyler means when he explains that all he's saying is that he has $4.25 (funnily enough, he says that just after the 4:25 mark).

As long as we're considering improvements, I have another unusual use for this routine. If you go back to my Scam School Meets Grey Matters...Still Yet Again! post, I feature the Purloined Objects/How to Catch a Thief! episode of Scam School, which I contributed to the show. It's not a bad routine as taught, but my post includes a tip which originated with magician Stewart James. This tip uses the Coin Coincidence/Trick That Fooled Einstein principle to take the Purloined Objects into the miracle class! I won't tip it here, so as not to ruin your joy of discovery.

June's snippets are ready!

This month, we're going back to some favorite topics, and provide some updates and new approaches.

• Let's start the snippets with our old friend Nim. The Puzzles.com site features a few Nim-based challenges. The Classic Nim challenge shouldn't pose any difficulty for regular Grey Matters readers.

Square Nim is a bit different. At first glance, it might seem to be identical to Chocolate Nim, but there are important differences to which you need to pay attention.

Circle Nim is a bit of a double challenge. First, you may need to try and figure it out. Second, the solution is images-only. Once you realize that different pairs of images are referring to games involving odd or even number starting points, it shouldn't be too hard to understand.

• Check out the Vanishing Leprechaun trick in the following video:



These are what are known as geometric vanishes, and can be explored further in places such as Archimedes' Laboratory and the Games column in the June 1989 issue of OMNI Magazine.

Mathematician Donald Knuth put his own spin on these by using the format to compose a poem called Disappearances. If you'd like to see just how challenging it is to compose a poem in geometric vanish form, you can try making your own in Mariano Tomatis' Magic Poems Editor.

• Back in July 2011, I wrote a post about hyperthymesia, a condition in which details about every day of one's life are remembered vividly. That post included a 60 Minutes report about several people with hyperthymesia, including Taxi star Marilu Henner. Earlier this year, 60 Minutes returned to the topic with a new story dubbed Memory Wizards. This updated report is definitely worth a look!

• If you're comfortable squaring 2-digit numbers, as taught in the Mental Gym, and you think you're ready to move on to squaring 3-digit numbers, try this startlingly simple technique from Mind Math:



That's all for June's snippets. I hope you have fun exploring them!

There's plenty of mental math shortcuts out there for addition, subtraction, and multiplication. The mental shortcuts for division are harder to find, but they are out there.

When you start asking about mental math shortcuts related to exponents, however, the only methods you find relate to taking roots, like my root extraction tutorial in the Mental Gym. What about actually taking numbers up to various powers instead?

WRAPPING YOUR HEAD AROUND EXPONENTS: Working out exponents seems scary, because most people are familiar with how quickly exponents become large numbers. You've probably heard a version of the classic legend about the reward given to the inventor of chess:



Too many people think of exponents as just repeated multiplying, but it's better to think of it as growth for a given amount of time. BetterExplained.com's article, Understanding Exponents (Why does 0^0 = 1?) is a great place to begin intuitively understanding the nature of exponents.

I've written before about mathematician and engineer Solomon Golomb, who challenged himself to be able to work out, or at least recall, the solution to any problem of the form x^y where x and y were any integers (whole numbers) from 1 to 10. In college, a professor mentioned the number 2²⁴, joking that "everybody knows what that is." When Solomon Golomb realized that 2²⁴ was the same as 8⁸, he was able to immediately reply, "Yes! It's 16,777,216!" The teacher was stunned to learn that it was the correct answer!

I may not get you that far in this post, but I think you'll be surprised just how far you can go with just a little extra mental training.

EASY EXPONENTS: There are a few easy exponents with which you should already be familiar. 1 to any power is always 1. Similarly, 10 to any power is simply 1 followed a number of zeroes equal to the power. 10² is 1 followed by 2 zeroes, or 100, 10³ is 1 followed by 3 zeroes, or 1,000, and so son. Also, any number to the first power is always itself.

Squaring, of course, is just multiplying a number by itself. When you learned multiplication starting with times tables, that included multiplying all the numbers from 1 to 10 by themselves, so from this point on, I'll assume you know these already.

CUBES: When a number is raised to the 3rd power, we say it's cubed. A cube is easily worked out by multiplying a number times it's own square. 2³ can be determined by multiplying 2 by the 4 (the square of 2) to get 8, and 3³ can be determined by multiplying 3 × 9 (the square of 3) to get 27.

After that, we start having to deal with 2-digit numbers by 1-digit numbers. 4³ is 4 × 16, and you might be fine working that out in your head, but what about 5³ (5 × 25) through 9³ (9 × 81)? Fortunately, Mental Math secrets is here to help you learn how to multiply 2-digit numbers by 1-digit numbers:



Once you've mastered this, you can easily work out cubes in your head! Even better, since we're only talking about 10 different cubes, regular practice will make them easy to recall, instead of calculate, so you can get them even quicker.

4TH POWER: Taking a number to the 4th power can be done by squaring the number, and then squaring the result you get. Once again, if you know your times tables, 2 and 3 are easy to take the 4th power. To get 2⁴, we square 2 to get 4, and then square 4 to get 16. For 3⁴, we square 3 to get 9 and then square 9 to get 81.

The problem comes, of course, when we need to square 2 digit number. For 4⁴, it's easy enough to do 4 squared to get 16, but how do we square 16? This problem continues up to 9⁴, for which you need to work out 81 squared. Fortunately, Harvey Mudd College Professor Arthur Benjamin is here to show you how to easily square 2-digit numbers:



Notice what the method of moving to the nearest multiple of 10 does - it turns 2-digit times 2-digit multiplications into 2-digit times 1-digit multiplication, which you learned how to do earlier! In fact, you can use those same techniques to help you work out these problems quickly.

Try this technique and practice working out the numbers 1 through 10 to the 4th power. You'll be amazed how quickly you're able to calculate, and before long just recall, each of these numbers.

5TH POWER: Once you're confident in your ability to work out 4th powers of the numbers in your head, you're ready for 5th powers.

To work out the 5th power of a number, you're going to take that number and multiply it by its own 4th power. 3⁵ is 3 × 3⁴, or 3...9...81, or 243. This is easy, as you've already mastered multiplying 2-digit numbers by 1-digit numbers by this point.

Multiplying numbers with 3 or more digits by a 1-digit number is similar to the process you learned earlier, but you do need to ready to work with more digits. Mental Math Secrets posted this 3-digit by 1-digit multiplication video on their site to help you learn this technique more effectively. Once you get the hang of this, multiplying 4-digit numbers by 1-digit numbers also shouldn't be that difficult.

5th powers also have a neat pattern: Each number 1 through 10, when taken to the 5th power, ends with the same digit as the number with which you started. 2⁵ ends in 2, 3⁵ ends in 3, and so on.

6TH POWER: If you've made it to the point where you can do 5th powers in your head, you may want to stop there. If you're ready for another challenge, however, then you may want to consider learning 6th powers.

To take a number to the 6th power, you'll need to find a number's cube, and then square it. Remember, however, that some of the cubes up to 9 are 3-digit numbers, so this will require the ability to square 3-digit numbers.

Squaring 3-digit numbers was briefly described above in the Arthur Benjamin video, but there are a few points you should know before you practice. First, you should be able to square all the numbers from 1 through 50 as fast as possible. Your adjustments will always be up or down by no more than 50, so this is an essential skill. Second, you'll need to be comfortable multiplying 3-digit numbers by 1-digit numbers.

Finally, when applying Professor Benjamin's technique for squaring 3-digit numbers, there's an easy to way to get that 2nd number you're going to multiply by that multiple of 100. Simply take the last two digits of the number you're squaring and double them, using the hundreds digit plus the final two digits of this doubling (if the number is greater than 100).

For example, when trying to square 729, you're obviously going to multiply by 700, but what's the other number? Simply double 29 (the last 2 digit of 729) to get 58, so you know the other number you need must be 758. What about 343? 43 doubled is 86, so you'll multiply 300 times 386. Once you see the pattern, it's easy to grasp.

Taking the numbers 1 through 10 to the 6th power is as far as I'm going in this post, so you can practice to the level you want. If you find any handy tips or tricks for doing exponents in mental math, I'd love to hear about them in the comments!

One of my major pet peeves, as many Grey Matters know, is the portrayal of memory and understanding as opposite ways to learn, instead of simply two approaches that can aid each other.

Today, we turn to another pet peeve of mine, the classic myth about people using only about 10% of their brains!

TED-Ed recently posted a wonderful video, titled What percentage of your brain do you use?, that takes apart the classic 10% myth from many different angles. It's quite an eye opener!



If you're registered at the TED-Ed site, you can delve into the full lesson here.

That's all for now, but I'm glad to finally have a decent reference to which I can refer people about this all-too pervasive myth. Enjoy this food for thought!

For January's snippets, I'm featuring an unusual mix.

This time around, I've got 3 different things for you: Math, memory...and Macs?!?

• Numberphile took a breather from their usual number videos to do something a bit different. They interviewed UC Berkeley professor Edward Frenkel with the question, “Why do people hate mathematics?” It's an interesting topic and well worth your time:



• In the video above, they talk about the important roles of math teachers. Longtime Grey Matters readers know that I'm not just a big proponent of memorizing, but rather memorizing along with understanding. Above and beyond great sites that aid in mathematical understanding, such as BetterExplained and Plus magazine, there's also an excellent free ebook called Nix The Trix. It's aimed at students who are great with shortcuts, but never took the time to understand the foundations of what those tricks are actually doing. It can help teachers undo the damage by showing how to teach the actual mathematical basis, which is also a great help in understanding when to use the math tricks.

• Almost just in time for this month's snippets, Reddit featured an interesting and popular thread asking, “What are some things worth memorizing?” Yes, of course, there are the usual array of sarcastic and silly answers, but if you take the time to wade through some of the roughly 12,000 comments (at this writing), there are some great ideas. I won't rob you of the joy of discovery, especially as the reply you most enjoy may not even exist yet as I write this!

• If you've ever memorized something with the help of spaced learning, where the concept you're trying to memorize is reinforced 3 times at spaced intervals, you know how powerful it can be. There's now an online web service called MemStash which help you do this almost automatically. You save things you wish to remember by highlighting them in an online page, and then clicking a special MemStash bookmarklet. After that, they'll send you 3 reminders at spaced intervals, which can help you recall what you saved!

• OK, this last snippet isn't really along the usual Grey Matters topics, but I thought it would be fun to sneak it in. 30 years ago this week, the Apple Macintosh computer first came on the market. During Super Bowl XVIII on January 22, 1984, they aired their now-classic 1984 ad, announcing the upcoming release of the Macintosh on January 24th. The lesser-known January 24, 1984 introduction of the Macintosh has also been preserved on video:



That's all for this month's snippets. I hope you enjoy them!

Many in the US are enjoying a lazy 4-day weekend as I write this. That being the case, I'll keep the feats relatively simple.

In this post, you'll find out how to easily give others a new perspective by looking at time and space in new ways!

EARTH PHASE FROM THE MOON: If you've practiced working out the moon phase for any date in your head, whether you do the full version, or just memorized how to do it for 1 particular year, this feat is surprisingly simple.

Once you've determined the phase of the moon on a given date, the phase of the Earth as seen from the moon will be exactly the opposite phase! If the moon, as seen from the Earth, is in a full moon, then the Earth, as viewed from the moon, will be a “New Earth” (the Earth will be unlit). If the moon is in a waxing gibbous phase (more than 50% lit, and getting brighter each night), then the Earth, as seen from the moon, will be in a waning crescent phase (the Earth will be less than 50% lit, and getting darker each night).

Why does it work out this way? Take a look at the moon phase diagram below. Pick a phase, and follow that phase's line from the Earth to the moon, and imagine extending it through the moon. Imagine yourself out in space, along that line, looking at the opposite side of the moon that everyone on Earth sees. It's not hard to understand that the moon on this side must be in the opposite phase. If one side is getting brighter, the other side must be getting darker, and vice-versa.

Now, imagine yourself on that same line, but now you're between the Earth and the moon, facing the Earth. The sun is far enough away (90+ million miles!) that it's going to be lighting the opposite side of the moon and the Earth in the same way.



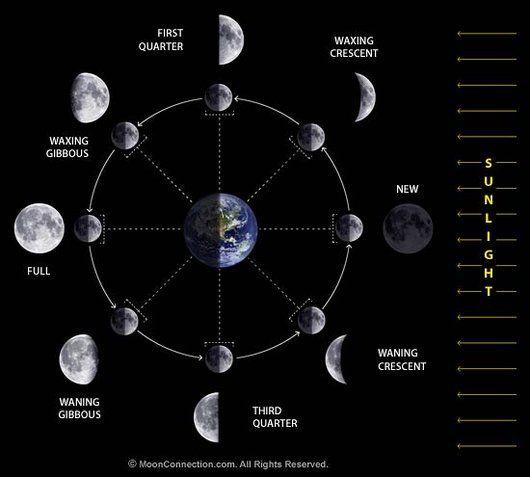
Just as in the original feat, you can verify this with Wolfram Alpha. If someone asks for the moon phase for, say, December 10, 2014, you would use the standard feat to estimate that the moon would be 19 days old (18-20 days old, including the margin of error), so you'd know it's in a waning gibbous phase, which means the moon is more than 50% lit, and getting darker each night.

Conversely, the Earth, as viewed from the moon, must be in a waxing crescent phase, so the Earth is less than 50% lit, and getting brighter each night. Wolfram Alpha can verify this for you.

1 MILLION SECONDS AGO: When you hear large numbers tossed around, it's really hard to get a sense of scale. How big is something like 1 million? To put it into perspective, imagine we're talking about 1 million seconds. When was it 1 million seconds ago?

Determining this isn't hard, especially if you just want to give the correct date. 1 million seconds is roughly 11.5 days. You can work out in your head what day 12 days ago was, or just cheat and use Wolfram Alpha to find out. If your local time is 1:46 PM or before, 1 million seconds ago was 12 days ago. If your local time is 1:47 PM or after, 1 million seconds ago was 11 days ago.

I'm writing this paragraph on December 1st, 2013, at about 11:45 AM local time, so 1 million seconds ago was November 19th, 2013. If I'm asked this afternoon at, say, 3:30 PM when 1 million seconds ago was, I'd say it was November 20, 2013, instead, because that is after 1:47 PM.

If you're interested in giving the exact minute, take the current time, add 13 minutes, then add 10 hours. 1 million seconds before December 1st at 11:45 AM would be November 19th of the same year at 9:58 PM, because 11:45 AM plus 13 minutes is 11:58 AM, and 10 hours after that is 9:58 PM.

If you're challenged to work out the exact second it was 1 million seconds ago, add 13 minutes and 20 seconds before adding the 10 hours. On 1:46:40 PM local time on any given day, 1 million seconds ago was exactly midnight, heading into 11 days ago.

As always, people can verify your answer using Wolfram Alpha.

1 BILLION SECONDS AGO: Since we're talking about large numbers, many people don't realize the difference in scale between 1 million and 1 billion, so when was 1 billion seconds ago?

1 billion seconds is over 31 years ago, so don't try and work out the exact date in your head. For this one, just look it up in Wolfram Alpha. As I write this on December 1, 2013, 1 billion seconds ago was March 25, 1982.

Working out the exact time is even simpler for 1 billion seconds ago, as it happens. First, add 13 minutes (and 20 seconds, if desired), just as before, but subtract 2 hours instead of adding 10 hours. December 1, 2013 at 11:45 AM minus 1 billion seconds is March 25, 1982 at 9:58 AM. Yes, your calculations can be verified with Wolfram Alpha.

You can make older dates like this more vivid by looking up those days on Wolfram Alpha or Wikipedia's year pages. For example, just a quick scan of those pages, I can remember that Danica Patrick was born, the first computer virus was only 2 months old, and the Vietnam Veteran's Memorial in Washington, D.C. would be opened the next day for the very first time.

1 TRILLION SECONDS AGO: 1 trillion seconds ago is the easiest, because that was 31,689 years ago, before modern clocks or calendars existed. This is roughly around 30,000 BCE, so ideas like the bow and arrow were still new, and not a single person was living in Japan yet. Obviously, if you include this, it's more for the sense of scale as compared to 1 million and 1 billion seconds ago.

If you like more mind-blowing changes in perspective, check out my Astronomical Scale post, and be ready for even more surprises!

Regular Grey Matters readers realize that I'm not just a fan of learning about new concepts and ideas, but also of finding clearer and better ways to communicate those concepts and ideas to others.

When you get that aha! moment where you truly understand a concept, or at least start to do so, there's a wonderful feeling of getting past the frustration. In today's post, we'll look at some places that encourage that moment by teaching various concepts clearly and simply.

One of the topics people have a tough time with is physics, the study of matter and how it moves through time and space. The MinutePhysics YouTube channel does a wonderful job of giving an overview of even seemingly difficult physics concepts. For example, this video explains how Einstein deduced the existence, and even the size, of atoms:



For a wider variety of topics, there's CGP Grey's YouTube channel. CGP Grey has a knack for picking topics that make you say, “I've often wondered about that, but never took the time to find out!” For example, as I write this, it's a leap year, so what exactly is the deal with leap years?



Although it's not a YouTube channel per se, the various videos of the “Charlievision” sequences from the show Numb3rs are a wonderful way of explaining complex mathematical concepts. Here's how Numb3rs summed up what is known as the knapsack problem:



Video isn't the only way to grasp new concepts, of course. I've referred to BetterExplained.com numerous times, in praise of their way of presenting insights. At the beginning of A Visual, Intuitive Guide to Imaginary Numbers, the author explains some of his secrets, which focus on analogies, relationships, and visual diagrams whenever possible.

One part of BetterExplained.com you may not be as familiar with, however, is their aha! moment section, where you can share with others the insights that worked for you. As the video below explains, it's a sort of Twitter meets Wikipedia (Twittipedia?):



One of my favorite posts there shares a handy insight from purplemath.com for remembering how to determine the proper sign when multiplying with negative numbers:

good things (+) happening to good people (+): a good thing (+)
good things (+) happening to bad people (-): a bad thing
bad things (-) happening to good people (+): a bad thing
bad things (-) happening to bad people (-): a good thing (+)

Martin Gardner made many puzzles and magic tricks popular over the years.

This post focuses on one particular bar bet whose popularity seems to come and go like the tide. It involves nothing more than 3 glasses and someone to challenge.

Martin Gardner first wrote up this puzzle in his December 1963 Scientific American column. It was later reprinted in the “Parity Checks” chapter of Martin Gardner's 6th Book of Mathematical Diversions from Scientific American.

A brief write-up of it is also found in his book Entertaining Science Experiments with Everyday Objects under the name “Topsy-Turvy Tumblers,” and Google Books has made the Topsy-Turvy Tumblers page available online for free.

Usually, it's described with the objective as getting all 3 cups mouth up, but it's easy enough to alter the goal to getting all 3 cups mouth down, as in the following video:



Whether you decide your challenge will be to get all the cups face-up or face-down, the process is the same. The spectator must follow your action exactly, do everything in 3 moves, and wind up with the cups facing the same way as you.

The three moves are a throw-off. When you look at the alternating set-up at the beginning, it's easy to see that you could achieve the goal by just flipping the two outer cups. Once you realize this, it becomes an easy way to check that you have the cups set in the right position for the correct goal when you do it, and in the wrong position for the wrong goal when the other person does it.

The pattern of moves they have to follow is easy enough. Turn the two rightmost cups, followed by the two outer cups, followed by the two rightmost cups again. When performing this, you really only need to think of this as right-outer-right.

Most people who do this puzzle stop with this once they win their money or drink. There is, however, a little-known sequel to this puzzle. Martin Gardner and Karl Fulves developed it together, but taught it with pennies instead of cups, so few have made the connection between the two routines.

In the sequel, you bet that you can get all 3 glasses facing the same way while blindfolded, and without even knowing the arrangement of the glasses!

You explain that you are going to be blindfolded, or otherwise prevented from seeing and touching the cups (this could be done over the phone, if desired). You mention that since you'll be blindfolded, you need a little leeway and will instruct the other person to flip the glasses one at a time.

The original write-up is a little hard to find, but thankfully, it was printed up in the American Scientist article, “Puzzles and tricks from Martin Gardner inspire math and science,” which is available for free online. It was also discussed further in the January 2012 issue of the College Mathematics Journal, which is also available in full online, in an article by Ian Stewart titled, “Cups and Downs.”

How is this possible? The method is simply this: First, you tell them to flip the leftmost glass. Next, you tell them to flip the middle glass. At this point, you ask them whether all the glasses are facing the same way yet. If so, you stop, of course, and if not, ask them to flip the leftmost glass one more time. At this point, the glasses are guaranteed to all be facing the same way!

After the second flip, the step where you flip the middle glass, you may get lucky and hear audible gasps, indicating that the people are amazed you reached your goal so quickly without looking.

If you don't hear any reactions after the second flip, you'll need to ask a question without appearing to do so. The most effective way to do this is simply to ask, "The cups aren't all facing the same way, are they?" Note that this starts with a negative statement, and then asks the question briefly.

If they reply that the cups are NOT facing the same way, you simply say, “I didn't think so,” and then make the last flip. This way, it sounds to the audience like you knew that wasn't the case all along.

If they reply that the cups ARE all facing the same way now, you say, “I thought so! Thank you!” When it happens this way, it simply seems like you're confirming your success, and knew your challenge was complete!

The Ian Stewart article linked above explains the mathematics behind this in a very clear manner, largely with a simple diagram of a cube. The American Scientist article also features a 4-object flipping sequence in which 2 objects are flipped at a time, and it still takes 3 moves or less without looking.

Play around with this bet, and better yet, take the time to examine the mathematics behind it. For such a seemingly simple bit of business, it has plenty to teach.

In the past, I've discussed standard ways of visualizing mathematical concepts, including ways to grasp pi and get a sense of scale. What if you need to create your own visualizations, however?

It turns out our old friend Wolfram|Alpha is not only good at working out the math, but making it easier to grasp, as well.

Let's say you work for a company that's giving a holiday dinner for all 3,000 of its employees. As part of this dinner, there will be a drawing in which one of the employees will win a new car.

Your probability of winning the car, of course, is 1 in 3,000, and you really want to understand what this probability means. So, you might try working out 1/3,000 on Wolfram|Alpha, and seeing that this is equivalent to 0.03333%. All that really happened here is that you now have a different number to ponder. We know that a probability of 1 in 3,000 and 0.03333% is a slim chance, but it's all still too abstract.

As explained in the book Made To Stick, the trick to taking something abstract and making it concrete is to describe it in a way that can be experienced through the senses. My blog post on concreteness as it applies to magic performances goes into more detail, as well.

Instead of simply seeing the numbers as chances, then, what if we imagined the 3,000 represented some kind of physical space? For example, 3,000 might be pictured as 3,000 miles. What does 3,000 miles look like? Entering 3,000 miles in Wolfram|Alpha, we find out that this distance is about ¾ the length of the Amazon river, 20% longer than the distance from New York to Los Angeles, or about ⅛ the circumference of the earth at the equator.

It's getting easier to picture, but still a little hard to grasp. Let's try scaling things down to inches and see what happens. 3,000 inches is 10% longer than a Boeing 747, or the height of a 28-story building. That's good, but perhaps picturing it as an area, in square inches would be better.

Trying out 3,000 square inches, we see that this is roughly the size of the surface area of 11 NBA basketballs! This is a great image, as it's well within the realm of the average person's experience.

Remember, though, that we're trying to picture what 1 in 3,000 looks like, so we need to picture 1 square inch, as well. Wolfram|Alpha says that 1 square inch is about the size of a postage stamp, which is another great image.

Putting this together, we see that 1 in 3,000 can be pictured as the area of a postage stamp as compared to the surface area of 11 NBA basketballs! The image below gets the concept across quickly and directly.



Now that you can see the drawing as 11 basketballs covered in stamps, with a hope of the company picking your single stamp out of those, it's more easily understood.

It's best to play around with different ways of seeing the numbers involved to find the best image. Switching to metric, we see that 1 cm and 3,000 cm gives the image of the width of a CD case as compared to the length of the average blue whale. There's also the volume of volume of 26 M&MS as compared to 950 large eggs.

There's nothing that says you have to use physical space, either. 1 in 3,000 could just as easily be thought of as a single second out of an average college lecture, the mass of a ¾-full can of soda as compared to the that of 2 dairy cows, and more!

Note that, while discovering the images requires particular units of measurement, presenting the images doesn't require disclosing units at all. Stamps, basketballs, CD cases and blue whales become the units themselves. When exploring various images, you'll find that larger numbers generally require smaller units.

Play around with numbers you use, and see what you discover. If you find any numbers you've been able to make visual with amazing or amusing images, I'd love to hear about them in the comments!

While I often teach how to perform mental feats, especially over in the Mental Gym, it's also important to get an idea of how professionals present them.

In the past, you've seen how performers including Maths Busking and Dr. Arthur Benjamin. Today's post features some other professional performers of mental feats.

First, we have Anton Zellman, who has made a good long living as a trade show performers, using his mind to entertain and educate prospective clients.

Because it's one of my favorite mental challenges, check out his Day For Any Date video. Watch it once just to see the performance, then watch it again to pick up on the finer details. For example, note that he only gives dates in two recent years (1990 and 1991 in the video). I have no doubt he could handle many more years, but this limitation makes the feat current, quicker to do, and easier to verify using only the 2 calendars hanging behind him.

Also, notice that he teaches how to do the effect. He's not performing a magic trick, and he's not trying give the impression that he's superior to you. He's simply showing that the boundaries of the human mind are much bigger than we may think. The multiplication table analogy is a wonderful tool to get the idea across of how something that seems hard can quickly become much easier with practice.

Among Anton Zellman's other videos are ones on remembering names and memorizing lists. There are also other videos on Zellman's own website. Watch these, keeping in mind that he's working in an environment where you often have only seconds to attract and keep the attention of attendees. If you don't engage it, that's a potential lost sale.

Scott Flansburg, also known as the Human Calculator, performs amazing mathematical feats for business meeting, schools, and, fortunately for us, the occasional TV appearance. Here's his appearance on a Discovery Channel program called More Than Human:



A few of the feats you see on there can be learned right here on Grey Matters, including the long division feat and the cube root feat.

Again, the attitude here is important. Just like with Anton Zellman, he's sharing, not showing off. Indeed, the most recent tweet (well, retweet) from Scott Flansburg at this writing says:

RT @haleymillsap: Work for a cause, not for applause. Live life 2 express, not 2 impress. Don't strive 2 make your presence noticed, mak ...

— Scott Flansburg (@HumanCalculator) September 13, 2012

In the previous post, you learned about a disguised form of tic-tac-toe known simply as 15, and how to avoid losing if you go first.

In this post, you'll learn about the best strategy to use when you go second.

The game of 15 was written about repeatedly by Martin Gardner. His original Scientific American column on it is available in his book Mathematical Carnival. Gardner also discusses it briefly in Aha! Insight. In both sections, he also discusses other interesting ways to disguise tic-tac-toe.

You can also find out more variations of tuc-tac-toe, including 15, in the Games column of the August 1979 issue of OMNI magazine.

To start, you should understand that going second effectively puts you on defense. In this version of tic-tac-toe, as with regular tic-tac-toe, the first player has roughly twice as many opportunities to win than the second player does.

When going second in 15, the first move is simple. If the other player takes the 5 for their first move, your response is to take any even number. In this post, I'll assume you always take the 4, but the strategies can be adapted to any even number. If the other player takes anything EXCEPT the 5 for their first move, then you must take the 5.

Where do we go from here? Obviously, that depends on the other player's second move. We'll start by assuming they took something other than the 5.

Other person goes first, first move is anything EXCEPT a 5: The first thing you need to watch out for is whether that second card, combined with their first, can make a total of 15. If so, you need to block that potential win by taking that card. For example, if they took the 4 first, you took a 5, then they took a 3, you have to realize that their 4 and 3 can be a win with an 8, so you need to take the 8.

After the other player makes their third move, you need to check for a threatened win and block that, as well. If this move doesn't threaten a win, take any odd numbered card (except 5, of course). At this point, you'll have the 5 and an odd numbered card (such as the 9). If they're smart, they'll see this and block your win (Seeing your 5 and 9, they take the Ace, for example). If they do this, all you can do is block and draw. If they miss it, you've got a win!

In this post, you'll be introduced to a simple new game to play. Even better, it's a game you'll never lose.

It's not another version of Nim. This time, it's even sneakier!

Here's the rules of the game of 15:

1) Nine playing cards, with face values from Ace to nine, are face up on the table. The Ace always has a value of 1 in this game.

2) Players alternate taking turns, and on a given player's turn, they must take 1 card from the available group on the table. Neither player make take a card that has already been removed from the main pile.

3) The winner is the first person to obtain exactly 3 cards that add up to 15.

What kind of strategy would you use to win this game, or at least prevent losing?

You might be surprised to learn that you probably already know this game. It's a disguised version of (or in math terminology, it's isomorphic to) tic-tac-toe! How exactly does this relate to tic-tac-toe? Imagine the numbers 1 throught 9 arranged as a classic 3 by 3 magic square, so as to total 15 horizontally, vertically and diagonally:


This might seem like a hard arrangement to keep in memory, but it's easier if you picture the arrangements of even and odd numbers separately:



Now you can clearly see how the game relates to tic-tac-toe, and why it's played to 15. Since the other person doesn't realize what they're playing, this gives you an advantage.

In this version, however, the Ace through nine are laid out in a straight line in order, not the traditional crisscross pattern, so you can't see things as clearly as you would in a regular game. So, exactly what strategy should be used?

The proper strategy depends on whether you're going first or second. Let's start by assume you're going first. Following the classic strategies for X, as taught at chassandpoker.com and Wikihow, you'll want to take a corner square, which in this game equates to any even card (2, 4, 6, or 8).

When first learning this version of the game, always take a 4 when you go first. As you become more proficient in the game, you can start with any even card, but always starting with a particular card at first will help you get familiar with the essential.

There's only 2 different replies the other player can make:

1) They choose a 5: This is akin to taking the center square. You must reply by taking the 6 (the diagonally opposite corner). This might seem strange, as you'll have a 6 and 4 with no possibility of a 5, but you're setting a trap for them. If their 2nd move involves taking either the 8 or the 2 (a corner square, in other words), you've just won!

How? You take the sole remaining even number, which simultaneous blocks their possible win, and opens up 2 ways to win for you! When they block 1 way, you simply play the other to win.

Below is an animation of how the game looks in the standard form of tic-tac-toe. If you arrange the cards in the form of a magic square above, you'll be able to better follow along as I teach the strategies.

In the previous post, you learned how to work out a close estimate of the square root of any number up to 1,000.

Building on that skill, this post will show you how to go a little farther with this. You'll learn some extra touches, how to display this skill in context, and more!

Simplifying

February's snippets are here, and it's time to have a bit of fun with math!

• Let's start off with the founder of recreational mathematics, Martin Gardner. The January 2012 issue of The College Mathematics Journal is available for free online, and is dedicated to the work and memory of Martin Gardner! Being a math journal, it does get into some heavy math, but even if you don't care for that, there's still plenty of fun math-related experiments and puzzles you can try and enjoy. You can also access each article individually, if you prefer.

• There's a magic tumblr blog called 366 effects. The magic tricks posted there are largely classic effects, many of them math-based. You can even find a nod to Martin Gardner there! The author is very good about giving proper credit, as well.

• Over at Mind Your Decisions, there have been several interesting posts recently. The first one dealt with a puzzle about page numbers: A book has N pages, numbered the usual way, from 1 to N. The total number of digits in the page numbers is 2,808. How many pages does the book have? Back in 2000, this same puzzle was featured on Numericana, too. It's amazing how challenging such a simple problem quickly becomes.

• What's a better value for your money, a 12-inch diameter pizza, or two 8-inch diameter pizzas? One blogger was faced with that decision, did some mental math, and opted for the choice with more surface area, even winding up with a bonus! The Presh at the Mind Your Decisions blog had a similar experience, used a calculator and was beaten by someone using some quick mental math!

The latter version's mental math is especially impressive, as there are several layered mental math tricks used. The first trick is the elimination of constants. Pi, of course, is constant, and we can also assume the thickness is, as well, but those only matter when going for an exact answer, not a comparison. Next, notice that even though the formula for a circular area is Pi × radius², the mental math genius squared the diameters of the pizza. Again, because we're making a comparison, this is merely a scaled-up version of comparing the same circle's radius. Being able to work out problems such 14/9 in your head was taught here on Grey Matters back in 2009, and figuring out 1.5 squared is just a minor variation of squaring numbers that end in 5. Sometimes, in mental math, it's not just knowing what to do, but knowing what you don't need to do, as well.

• While we're focused on pizza and the Mind Your Decisions blog, here's how to play Nim with an unevenly-divided pizza, and ensure you wind up with the most pizza! If you like this game, make sure to check out my Nim posts. If it's tasty versions of Nim you're after, you'll particularly enjoy Chocolate Nim.

• I'll close with an answer, instead of a question. A poster over at Quora wondered what it was like to have an understanding of very advanced mathematics. An anonymous user provided a wonderfully clear and sincere answer that is a must-read. This is one of those posts that make you want to stand up in front of your monitor and clap, even though you know the author will never hear you.

It's one thing to learn an established memory technique. There are times when you want to remember something, but ready-made systems either can't handle the information itself, or bring up the information in a way you need.

The solution is to develop your own memory system. Not only is it possible, but if you do so, you'll have the satisfaction of not only remembering what you need, but also of knowing that you created the way to handle it.

What if you wanted to memorize all the 2-letter words allowed in Scrabble? That's the example we'll look at in this post.

A post titled “Hacking Scrabble,” provides a wonderful look at the approach one blogger used to meet this challenge.

Although it doesn't specifically say so in this article, I imagine that the person who wrote this article looked at the existing mnemonic systems used by Scrabble players. The most-used memory system here is called anamonics (a portmanteau of anagram and mnemonics), and is a way of recalling all the individual letters that could be added to a set group of letters to form legal Scrabble words.

The problem with using this approach is that anamonic lists generally start with three-letter words, not two.

The first step in working on the system was getting as much of the information needed together as possible. In this case, there's a readily-definable set of all the needed words:

aa ab ad ae ag ah ai al am an ar as at aw ax ay ba be bi bo
by ch da de di do ea ed ee ef eh el em en er es et ex fa fe
fy gi go gu ha he hi hm ho id if in io is it ja jo ka ki ko
ky la li lo ma me mi mm mo mu my na ne no nu ny ob od oe of
oh oi om on oo op or os ou ow ox oy pa pe pi po qi re sh si
so st ta te ti to ug uh um un up ur us ut we wo xi xu ya ye
yo yu za zo

a: abdeghilmnrstwxy   j: ao                 s: hiot
b: aeioy              k: aioy               t: aeio
c: h                  l: aio                u: ghmnprst
d: aeio               m: aeimouy            w: eo
e: adefhlmnrstx       n: aeouy              x: iu
f: aey                o: bdefhimnoprsuwxy   y: aeou
g: iou                p: aeio               z: ao
h: aeimo              q: i                 
i: dfnost             r: e

Magicians refer to what most would call “tricks” as “effects”. Anytime you have an effect, however, people are going to look for a cause.

The search for the cause naturally takes the audience from the effect itself to the performer themselves. In analyzing how to guide an audience's perceptions of cause and effect, superheroes often prove to be useful as an analytical tool.

In past times, ancient myths might have served the same purpose, as discussed in Joseph Campbell's Hero With A Thousand Faces. Indeed, summaries of his works can be found here (archived) and here (PDF). A fuller examination of this approach can be found in the Power of Myth 6-hour miniseries.

In an age where more people are familiar with Batman and Superman, as opposed to, say, Orpheus or Daedalus, superhero examples com much more readily to mind.

I was first made aware of this approach in Jon Armstrong's article “Superhero Theory”, published in the December 2004 issue of Genii. Sadly, there is no reprint of the exact article online, but it can be largely summed up with 4 major points:

• Superheroes are defined by their powers, to the extent that they're often named after them (e.g., Spiderman, the Flash).

• Audiences are familiar with what a particular superhero is capable of, so the heroes have certain expectations (without being made predictable), and they're made more memorable.

• Superheroes are limited by their powers (e.g., Batman doesn't have X-ray vision, Spiderman can't talk to sea creatures), creating focus, as well as opportunities for challenge.

• Speaking of limitations, many superheroes also have a weakness. How they deal with this weakness can be as engaging as how they use their superpowers.

(NOTE: Check out the other posts in The Secrets of Nim series.)

In past posts on Nim, I've discussed multi-pile standard Nim, multi-pile Misère Nim, and how to better visualize your moves for either kind of multi-pile Nim.

I've even discussed Werner Miller's brilliant Wise-Guy Nim variation, in which you allow the other player to decide whether the game will be standard or Misère, after which you subtly alter the rules in your favor.

What would happen if, instead of deciding the goal beforehand, the goal was declared after the game had started?

This unusual variation was developed by John Horton Conway (seen on video in my Iteration, Feedback, and Change: Artificial Life post), who dubbed it “Whim”.

Whim starts just like any other multi-pile Nim game, but with no determination as to whether the last person to remove a match is the winner (standard) or the loser (Misère).

The big difference with Whim is that only once during the game (NOT once per player), one player may, instead of removing objects, make a "Whim move", in which that player declares the goal to be standard or Misère. At this point, the goal of the game is frozen, and no further Whim moves can be made by either player. What effect does this have on strategy?

Since the strategy for both versions of multi-pile Nim are the same up until the final moves, you might figure that this would make analyzing the strategy easy. A complication quickly arises, however, when you realize that not only must a goal be declared at some point during the game, but that the temptation to use the Whim move is itself a factor.

Think about by imagining that you're playing first. Let's say you analyze the layout as I've taught in previous posts, and you determine that no objects need to be removed. If you're applying the strategy from my Visualizing Multi-pile Nim post, this would mean that you noted that all the powers of two are “paired up”.

In this case, it's easy. Instead of making a move, you make the Whim move, declaring the game to be either standard or Misère as you wish (on a whim, as it were). This forces the other player into a losing move either way (their move must “unpair” a power of two), and you will win the game as long as you stick to the proper strategy.

Now let's look at the opposite situation. You analyze the layout, and the normal strategy for Nim says you need to remove some objects. You could remove those objects, but the other player could make the Whim move, and then you're left with another losing position AND no way out (assuming the other player understands and plays regular Nim strategy). The only other possibility here is to intentionally make a losing move (a move that still leaves one of the powers of two “unpaired”)!

It gets worse. The other player must use the same logic, and make another losing move, too. As soon as either player fails to make what would ordinarily be a losing move, the other player can use the Whim move, and win the game from there.

Consider also that the goal must be declared at some point in the game, and the closer you get to the end, the more you need to know the goal in order to win the game. If both players are well versed in multi-pile Nim strategies, this becomes a very big problem, and one that's not easily analyzed.

Despite the difficulty of the analysis, the proper strategy is surprisingly simple and elegant.

You need to treat the Whim move as a separate pile of its own. If there is any pile consisting of 4 or more objects, you imagine that this imaginary “Whim pile” contains 1 object, and analyze the play as if this pile were actually there. Once every pile contains less than 4 objects, you need to think of the imaginary Whim pile as containing 2 objects.

The imaginary Whim pile only gets removed when one of the players makes the Whim move (declares the goal of the game). After that, play is straightforward for anyone who understands multi-pile Nim.

Due to the fact that the rules of Whim create an unusual hole, yet don't provide any apparent way to fill it (until the idea of imaginary piles is properly considered), seasoned Nim players can be stumped by these new rules, even after playing multiple games!