 A good puzzle has the counterintuitive quality of being very relaxing because of the thought you have to put into them. Here's a few good sites to lose yourself in some classic puzzles.
A good puzzle has the counterintuitive quality of being very relaxing because of the thought you have to put into them. Here's a few good sites to lose yourself in some classic puzzles.
• AMAZING Productions - Just started this month, this is a blog focused on mazes. Each post is a picture of a maze, and clicking on it will enlarge the picture. These are very high-quality original mazes, and should be printed out and given the time they deserve.
• Desert Labyrinth - Do you prefer your mazes in 3D? If so, check out Desert Labyrinth, a simple yet well-rendered 3D maze game that's different each time you play it! The interface is simple enough that it helps keep the focus on solving the maze, not figuring out how to play. You'll probably want to click on the compass to use the overhead view to help. You can even learn about how the game was built here.
• Puzzler's Paradise - If you enjoy logic puzzles that provide you with clues like, “Mary was 2 years older than the person who owned the dog” you'll enjoy this site. You can play online with the interactive grids, or print them out and work them by hand! New puzzles are posted often.
• Jigzone - There's nothing quite like a good old-fashioned jigsaw puzzle. There are several sites out there, but Jigzone has two important qualities over its competitors: 1) The interface is better designed and replicates the feel of the experience, and 2) It works even on devices that don't display Flash. As a matter of fact, the experience is even better on a touchscreen mobile device, since you're grabbing the pieces with your fingers directly!
• Puzzles.com - Looking for a wider variety of puzzles? Then this is the place! From original new puzzles to classics from older puzzle books (including many from Martin Gardner), puzzle lovers should definitely bookmark this site and return regularly.
• Chess and Poker.com - If you enjoy the Mental Gym, you'll definitely enjoy this site. Besides strategy guides for its name sakes, it features guides for everything from Tic-Tac-Toe to Dominoes to Carcassonne! Many classic puzzles are also taught here, including Rubik's Cube, Sudoku, and the 15 Puzzle.
• Jaap's Puzzle Page - This one has been a Grey Matters favorite for a long time. It teaches how to solve a wide variety of commercially available puzzles. In many cases, you can play those same puzzles in online versions, and even share them on your own website! If you want to understand the math behind these puzzles, the site usually gives high-quality mathematical explanations, as well.
Do you have any favorite puzzles sites you'd like to share? Let's hear about them in the comments!





 (
(
 April 10th is both the anniversary of
April 10th is both the anniversary of 

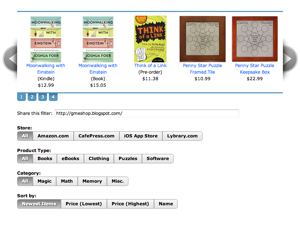
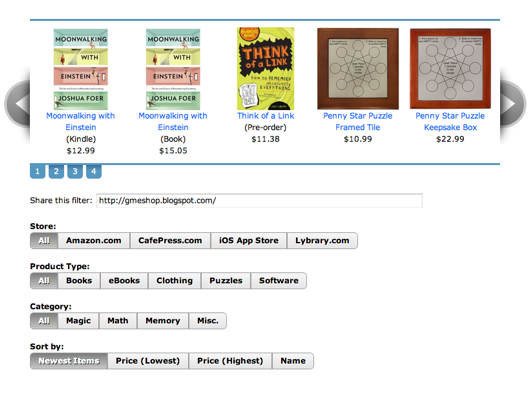

 Now that I've
Now that I've 

