I once met a man who didn't get too far in school. He explained that he had to leave school to help support his family, so the most advanced math he ever learned was multiplying and dividing by 2. He said he never got to understand more advanced things like fractions.
I once met a man who didn't get too far in school. He explained that he had to leave school to help support his family, so the most advanced math he ever learned was multiplying and dividing by 2. He said he never got to understand more advanced things like fractions.
Like me, you might expect that this guy wasn't too bright when it came to math, but he understood how to make the most of what he did know.
I chose two random numbers, not so high as to embarrass him, and asked, “So, if I asked you to multiply, say, 38 by 29, you couldn't do it?” He explained that he could, but he just had to simplify the problem in his own way.
He asked me to write down the problem on a piece of paper:
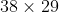
He reminded me that he had no problem multiplying and dividing by 2, so he explained that he was going to simplify the problem. He calculated, “38 divided by 2 is 19, so put 19 below the 38. 29 times 2 is 58, so put 58 below the 29."
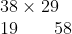
Now, I've seem multiplication simplified this way before, but since he'd mentioned he didn't care for fractions, I was wondering how he could simplify the problem any further.
Confidently, he continued, “Next, we do the same thing again. 19 divided by 2 is 9, so...” I interrupted, “19 divided by 2 is 9½, not 9.” He repeated that he never could deal with fractions, so he just told me to forget the fraction, and just put down 9.
I had to snicker a little, as I couldn't see how this would work. I then did as I was told, put the 9 down, and then put down the double of 58 he'd calculated, 116.
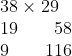
He continued in this manner, always getting the doubling right, but putting down things like 4 has half of 9.
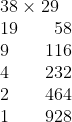
I was about to explain that, due to the lack of fractions, the problem didn't come down to 1 times 928, so 928 wasn't the correct answer, when he stopped me. He explained he wasn't finished yet, and said that he was no going to run through the left column and idenetify which numbers as odd or even.
At this point, I was intrigued, as I couldn't see how he was going to get any kind of answer to the problem.
He explained that he was going to mark a little 0 next to the even numbers, and a little 1 next to the odd numbers. He quickly went down the column, muttering, “19 odd, 9 odd, 4 even...” and marking them accordingly:
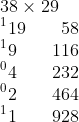
"Now what?” I wondered out loud. He replied, “Now, I add up ONLY the numbers in the right column whose numbers in the left column are marked with a 1! According to what we have on the paper, that's 58 + 116 + 928."
Instead of writing the answer and carrying all the values, he did the addition problem in his head by working from left to right, starting in the hundreds column! He said, “100...plus 900 is 1000...plus 50 is 1050...plus 10 is 1060...plus 20 is 1080...plus 8 is 1088...plus 6 is 1094...plus 8 is 1102! That's it!"
"That's what?” I asked as he wrote the total proudly below the other numbers. He explained, “The answer to your multiplication problem, 38 times 29!"
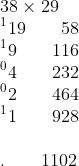
I was astounded. Double checking, I found that not only did 58 + 116 + 928 equal 1102, but that 38 times 29 was 1102, as well!” His way of working through the problem was strange, but I had to admit it worked!
"There's more!” he announced, while I was still recovering from the shock. He pointed out that we hadn't identified one of the numbers on the left as odd or even, and quickly marked 38 with a 0, denoting it was even.
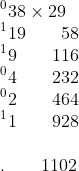
He then asked if I would read off the 1s and 0s column in order, reading from the bottom up. I verbalized, “100110.” This man, with a gleam in his eye, inquired, “You do realize that's 38 in binary, don't you?” Sure enough, Wolfram|Alpha backed him up on this.
"How could you possibly know about binary? I wondered. He joked, “Originally, I figured computers were beyond me, but once it was explained that they dealt mainly in powers of 2, and they had difficulty with fractions, too, I could instantly relate."
"Since school, of course, I learned about a few more things about math here and there, such as factorials. You know, 4 factorial is 4 × 3 × 2 × 1, or 24. 5 factorial is 5 × 4 × 3 × 2 × 1, or 120, and so on,” he recalled.
After I stated that I was familiar with them, he pointed out that when you work with larger numbers like that, you tend to get more and more multiples of 5, and of course many more even numbers, so factorials of numbers larger than 5 would always ended in 0. The factorial of larger numbers, of course, ended in many zeroes.
He then explained that calculations like this helped him work out exactly how many zeros would be at the end of a number's factorial. I was confused, but I no longer doubted him. He added, “We've been ignoring the 29 over there, so let's work out how many zeroes are at the end of 29 factorial. I'll start with 58, and erase the 1 rightmost digit from it, leaving 5 there. With the number below it, I'll erase the 2 rightmost digits. In the numbers below, I'll erase the 3 rightmost digits, and so on.” When he'd finished, the paper looked like this:
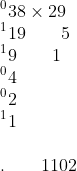
Using the remaining 5 and 1, he simply added them up to get 6, and claimed that 29 factorial had exactly 6 zeroes at the end of it (known as trailing zeroes). I had Wolfram|Alpha work out 29 factorial, and sure enough, while there were 7 zeroes in the entire number, exactly 6 of them were trailing zeroes. Embarrassingly, he pointed out that I could have asked Wolfram|Alpha about the zeroes directly, and save myself the trouble of counting them.
Like I wrote earlier, this guy may not have known much, but he could definitely make the most of what he did know.
---
OK, it's time to admit I lied about this guy. He's completely made up for the purposes of storytelling.
The math, however, is 100% real. The process of doubling and halving numbers, and adding only particular numbers is commonly referred to as “Russian Peasant Multiplication.” I discuss both this and the halving method to convert to binary last year, in October's Powers of 2 post. I first discussed this approach to the trailing zeroes phase last December.
Amazingly the process above, once understood, works for multiplying any two whole numbers. Unlike many mathematical feats taught on Grey Matters, the focus is not on speed or mental ability, but rather the sheer variety, power, and unexpected simplicity that can be derived from just a single math problem.
Try it out, have fun, and explore this unusual approach to math.

 When you first learn memory techniques, you also tend to apply them to a small set of standard lists, such as presidents, monarchs, countries, states, capitals, and so on.
When you first learn memory techniques, you also tend to apply them to a small set of standard lists, such as presidents, monarchs, countries, states, capitals, and so on.