This is the last post I'll make in 2013, so it's time to take a look back at the year in posts.
This is the last post I'll make in 2013, so it's time to take a look back at the year in posts.
There was a lot to go over this year, so I can't hit every post, but I think you'll enjoy the highlights I've chosen!
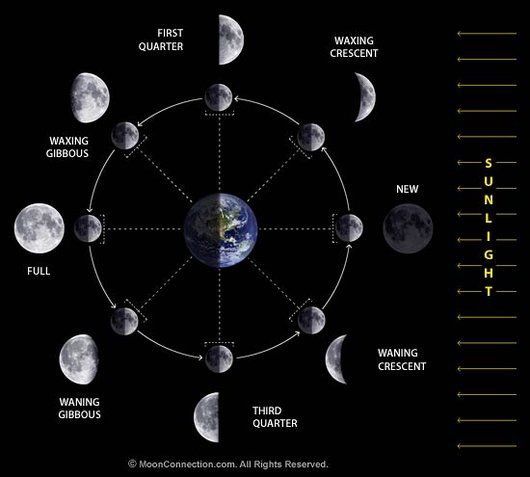
JANUARY: I kicked the year off with the announcement of my new Moon Phase For Any Date tutorial. Closely related to the moon tutorial was the lesson on how to work out the date of Easter for any date.
I also made several happy discoveries, including the release of James Burke's unedited documentaries on YouTube, and a maze programming tutorial I hadn't seen since I was a teenager!
FEBRUARY: February seemed to be a month for mental math tutorials. Besides a few quick feats, you learned about verifying prime numbers mentally, and the unusual technique of leapfrog division. Just for fun, we even brought Pi digits to life!
MARCH: We celebrated Grey Matters' 8th blogiversary with the most posts of any month in 2013! There were several offbeat memory challenges, and numerous offbeat math lessons, such as continued fractions, getting the most out of a single equation, untangling ropes mathematically, and even Scam School's lessons about cube roots.
APRIL: This month was quiet, but we still managed to cover new uses for old calculators. With Scam School's help, there were even lessons on memorizing a list of 20 items and an impressive mobile phone magic routine!
MAY: We returned to the basics at this point in the year. YouTublerone's memory technique videos made taught in a vivid way, and mental adjustments between the Gregorian and Julian calendars were made clearer. Learning to demonstrate mental feats in an entertaining way was also on the agenda.
JUNE: James Grime shared a fun way to predict sums, and Mel Stover's work was finally given due respect on Grey Matters. An interesting lesson on how to remember and calculate temperature conversions was also one of June's highlights.
JULY: After the previous month's temperature conversion post, a few new additions were introduced to make this easier. Multiplying by 10⁄9 was made simpler, and a technique developed for this was expanded to make numerous other mental math feats easier. Our favorite game Nim also returned.
AUGUST: The main focus of this month was a mystery feat! First, a technique for mentally multiplying by 63 was taught, followed immediately by how to mentally multiply by 72. What skill could possibly require these two abilities? I won't ruin it for you, but the answer can be found here.
SEPTEMBER: Just like May dealt with the basics, September brought complex concepts down to Earth, literally, in some cases. Quick magic tricks were an early treat, and Mental Floss' Be More Interesting gallery presented an entire buffet of techniques. Logarithms and astronomy were also explored and clarified.
OCTOBER: Picking up from September, memorizing the elements, and understanding them better with help from TED-Ed videos was the order of the day. Untangling family trees with help from Wolfram Alpha was another challenge we took on. Once again, Nim, this time in finger-dart form, put in another appearance on Grey Matters.
NOVEMBER: As the holiday season drew near, Dr. Arthur Benjamin seemed to take over the blog. His performance and lecture about mental math techniques was released shortly before his fun lecture about fibonacci numbers. Inspired by this, I also taught how to work out 3-digit cube roots, along with some handy tips and tricks.
DECEMBER: As the year drew to a close, I paused for a post about time, space, and perspective, and looked back at some classic programs that helped clarify history, math, and more. The Pebbling The Chessboard problem rounded out the year with a good look at how to turn a problem into its mathematical equivalent.
Now, it's time to start looking forward to 2014, when we'll wind up 9 years of posts, and begin working on the 10th! I hope you'll join me here on Grey Matters!

 It's not always easy to see how the mathematics of a problem connects to the problem itself.
It's not always easy to see how the mathematics of a problem connects to the problem itself.