In my previous post, I showed you how other math geeks look at Halloween. Now, we're going to put your Halloween smarts to the test!
In my previous post, I showed you how other math geeks look at Halloween. Now, we're going to put your Halloween smarts to the test!
When I would come home for trick-or-treating with friends, instead of diving into our candy, we'd start trading. For example, I might trade my M&Ms, a Mars bar, and a Reese's all for my friend's single Hershey bar.
It's a little tricky trying to trade candy over the internet, so I've got a puzzle version for you, in which we're going to trade letters for numbers. The object of this candy equation is to replace each letter with a number so that the equation is true.
The rules are as follows:
• Each letter represents only one digit, 0-9, throughout the problem.
• Different letters represent different digits, and no two letters represent the same digit.
• Any letter that represents the leftmost digit in a number never represents 0.
• When solved, the equation must be true.
• There is only one possible solution.
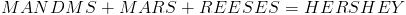
I'll post the answer to this candy puzzle in my next post.
Another part of the fun of Halloween is going out and seeing all the carved pumpkins. Flickr user freeflower has generously shared these pumpkins with us. These pumpkins are from a contest held every year in her neighborhood where you must vote on your favorite pumpkin before getting your treat.
Before you even get to see the pumpkins, though, you must unscramble them. Click or touch (yes, this works on mobile devices) on any block next to the empty space, and that block will slide into the empty space. The Shuffle button both mixes the pieces and resets the move counter, while the Original button shows the finished picture.

Looking for still more Halloween puzzles to strain your brain?
Check these out:
Halloween jigsaw puzzle gallery (JigZone)
Brain Game: Sweet Things (mental_floss)
Halloween Spot The Difference (Marion Cole)
A Hangman Haunting (pjnation)
Halloween World Ladder (sporcle)
Did you manage to solve any of these puzzles? If so, let me know how you did in the comments!


 I've talked about
I've talked about